理論概述
 風險中性
風險中性風險中性者並不介意一項投機是否具有比較確定或者不那么確定的結果。他們只是根據預期的貨幣價值來選擇投機,特別而言,他們要使期望貨幣價值最大化。
原理解釋
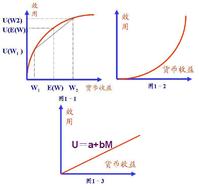 風險中性
風險中性是考克斯(Cox,J.C.)和羅斯於1976年推導期權定價公式時建立的。由於這種定價原理與投資者的風險制度無關,從而推廣到對任何衍生證券都適用,所以在以後的衍生證券的定價推導中,都接受了這樣的前提條件,就是所有投資者都是風險中性的,或者是在一個風險中性的經濟環境中決定價格,並且這個價格的決定,又是適用於任何一種風險志度的投資者。
關於這個原理,有著一些不同的解釋,從而更清淅了衍生證券定價的分析過程。首先,在風險中性的經濟環境中,投資者並不要求任何的風險補償或風險報酬,所以基礎證券與衍生證券的期望收益率都恰好等於無風險利率;其次,正由於不存在任何的風險補償或風險報酬,市場的貼現率也恰好等於無風險利率,所以基礎證券或衍生證券的任何盈虧經無風險利率的貼現就是它們的現值;最後,利用無風險利率貼現的風險中性定價過程是鞅(Martingle)。或者現值的風險中性定價方法是鞅定價方法(MartingalePricingTechnique)。
要點
(1)影響期權價格的因素主要是未來的股票價格的變化
(2)關鍵是確定上行機率和下行機率
假設投資者對待風險的態度是中性的,所有證券的預期收益率都應當是無風險利率。風險中性的投資者不需要額外的收益補償其承擔的風險。在風險中性的世界裡,將期望值用無風險利率折現,可以獲得現金流量的現值。
在這種情況下,期望報酬率應符合下列公式:期望報酬率=(上行機率×上行時收益率)+(下行機率×下行時收益率)
假設股票不派發紅利,股票價格的上升百分比就是股票投資的收益率,因此:期望報酬率=(上行機率×股價上升百分比)+(下行機率×股價下降百分比)
根據這個原理,在期權定價時,只要先求出期權執行日的期望值,然後,使用無風險利率折現,就可以求出期權的現值。
風險中性原理計算期權價值的基本步驟
1、確定可能的到期日股票價格
2、根據執行價格計算確定到期日期權價值
3、計算上行機率和下行機率期望報酬率=(上行機率×股價上升百分比)+(下行機率×股價下降百分比)
4.計算期權價值期權價值=(上行機率×上行時的到期日價值+下行機率×下行時的到期日價值)/(1+r
策略組合
 風險中性
風險中性在一個無套利(機會)均衡市場中,由風險資產與無風險資產適當配比構造投資組合,其現金流特徵等於無風險資產加上無風險收益,這是期權理論核心思想。中國證券市場還不存在衍生品交易機制,即不存在股指期貨及看跌期權,“股票+看跌期權”及“股票+股指期貨”等現金流動態複製策略無法實現,組合保險策略依據中國證券市場條件,用“股票+國債”或“股票+現金(保證金)”來複製“股票+看跌期權”及“看漲期權+現金(保證金)”,前者是規避股票下跌風險,後者是規避通貨膨脹風險。當投資組合構造完成後,一般賬戶中會暫留一定比例現金或國債,股票市值加現金反映出了任何時期的賬戶現金流價值(或市值)特徵,賬戶市值會隨股票市值波動而變化,風險中性策略組合保險就是用部分(一定比例)股票複製看跌期權,用部分現金複製看漲期權,如果股票加現金(或國債)的賬戶市值用如下公式表示:
VP=∑WS×PS+∑WB×PB
PS—股票價格,WS—股票數量,PB—債券面值,WB—債券數量
構造風險中性策略組合保險的賬戶市值就可用如下公式表示:
VP=∑WS×PS+∑WB×PB+∑WC×VC+∑WP×VP
WC—複製看漲期權的數量,
WP—複製看跌期權的數量,
VC—看漲期權內涵價值,即maxs-ko
VP—看跌期權內涵價值,即maxk-s0
Ep=∑WC×VC+WP×VP為連續複製狀態下的無風險收益,Ep在風險中性策略組合保險中稱為保險額,Ep的設計應針對賬戶中風險資產暴露的最大風險,
VB×Ep=VS×σd×N(1-x%)×T1/2當投資組合中的風險資產市值VS接近於無風險資產市值VB時,Ep=VS×σd×N(1-x%)×T1/2
一般情況下:
Ep=VS÷VB×σd×N(1-x%)×T1/2
此時的賬戶價值不隨股票價格波動而變化,也不隨市場波動而變化,賬戶價值由帳戶未來價值用無風險收益率貼現得到的現值表示。風險中性策略組合保險複製無風險收益Ep的過程,就是通過複製賣權與買權的價格實現,如果風險市值由WS×PS表示,其未來的市值由WS'×PP'表示,PP'就是賣權價格,即可表示PP'=(WS÷WS')×PS×(1+Ep),如果無風險市值由WB×PB表示,其未來的市值由WB'×PB'表示,PB'就是買權價格,PB'=(WB/WB')×PB×(1+Ep)。
求證試驗
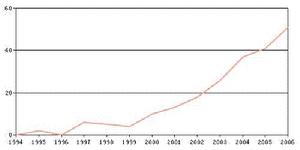 風險中性
風險中性期權定價模型是期權理論分析的一個重要內容,它是金融工程研究的基礎。1973年金融學家費雪·布萊克(FischerBlack)和邁倫·斯科爾斯(Myronscholes)在美國《政治經濟學》上發表了論文《期權和公司債務的定價》,給出了歐式股票看漲期權的定價公式,即今天所稱的Black2Scholes模型,該模型被稱為“不僅在金融領域,而且在整個經濟領域中最成功的理論”,斯科爾斯因此和美國哈佛商學院的教授羅伯特·默頓(BobertC.Merton)獲得了第29屆諾貝爾經濟學獎。但Black2Scholes期權定價公式的推導過程是相當複雜的,需要用到隨機過程、隨機微分方程求解等高深的數學工具知識。Black2Scholes公式的兩個新穎和簡潔的推導,即在風險中性假設下來推導出Black2Scholes
基本假設和記號
藉助於Black2Scholes模型的原始假設條件:
(1)期權是股票的歐式看漲期權,其執行價格是K,記當前時刻為t,期權到期時間為T,股票當前價格是S,時刻的價格是ST。
(2)股票價格遵循幾何布朗運動,即logST-logS~Φ[(μ-σ22(T-t),σT-t]其中Φ(m,n)表示均值為m,標準差為n的常態分配。
(3)允許使用全部所得賣空衍生證券。
(4)無交易費用或稅收。
(5)在衍生證券的有效期內沒有紅利支付。
(6)不存在無風險套利機會。
(7)證券交易是連續的。
(8)無風險利率是常數且對所有到期日都相同。
再假設投資者都是風險中性的,在風險中性世界裡,股票的預期收益率μ等於無風險利率r,則由假設(2),得到
logST-logS~Φr-σ2(T-t),σT-t
由對數常態分配的特性,可知ST的期望值E(ST)表示為E(ST)=Ser(T-t)。對於不支付紅利股票的歐式看漲期權,它在到期日的價值為CT=max{ST-K,0},期權當前價格C應是E(CT)以無風險利率貼現的結果,即C=e-r(T-t)E(CT)=e-r(T-t)E(max(ST-K,0))
實踐套用
 風險中性
風險中性風險中性組合的概念
知道,期權的價值由標的資產價格、標的資產價格的波動率、執行價格、到期時間及無風險利率決定,其中任一因素的變動都會影響到期權的價值。但是,可以構造基於若干期權或期權與標的資產的組合,使其價值不受其中一些因素變動的影響,這樣的組合稱之為風險中性組合。常見的有Delta中性組合、Delta-Gamma中性組合及Delta-Gamma-Vega中性組合。這裡僅討論前兩類組合。
Delta中性組合的構造
Delta是衡量標的資產價格變動對期權價格影響程度的一個參數,且組合頭寸的Delta值具有可加性。即如果計
算出組合頭寸中所有期權的Delta值,並將他們相加,就可以得出組合頭寸的Delta值,它表明標的股票價格運動一點時,組合價值的增加或減少額。對於一個Delta值為0或近似為0的頭寸稱為Delta中性頭寸,如果一個頭寸是Delta中性的,那么在短期內對於標的資產價格較小的變化,組合將不會面臨損失的風險或潛在的收益。
例如,已知標的股票的當前價格為S=98,r=6%,!=0.3。當前時間為3月份。某投資者以4.65買入一份6月100買
權,同時以1.54的價格賣出兩份6月110買權,以構造空頭買權比率價差組合。可以看到,以1:2的組合來構造空頭買權比率價差(組合1),一般而言,其Delta值並不為零。這表明,標的股票價格的變動將影響組合的價值。如果要構造Delta中性組合,可以按如下方式構造:做多1份6月100買權,同時做空2.22份6月110買權。這樣,新
 風險中性
風險中性的比率價差組合的Delta值為:0.508-0.229×2.22=0
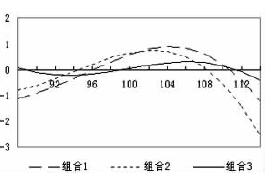
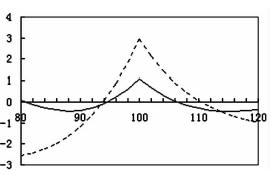
考察一周后,股價變動對兩個組合價值的不同影響,虛線是在一周后不同的股票價格(微小變化)時1:2組合的盈
虧情況,實線是1:2.22組合的盈虧情況。可以看到,實線的波動幅度較虛線的波動幅度要小得多。這說明通過構造Delta中性組合,確實能保證在較短時間內,在股價波動不大情況下,組合價值的穩定性,即面臨較小的風險。
然而,如果股價大幅上漲或下跌,或者隨著時間的流逝,或者隱含波動率變動,各期權的Delta將發生變化。一旦這些Delta變化,組合將不再是Delta中性。從而它將面臨著風險。從敏感性參數來看,無論是1:2,還是1:2.22組合,其Gamma均不為零,這說明隨著時間的推移及標的股票價格的運動,原先的Delta中性將不再是中性的了。這時,為了實現波動率套利,必須考慮Delta-Gamma中性。Delta-Gamma中性組合的構造仍然考慮以上情形,當前時間為3月份,標的股票的價格S=98,r=6%,!=0.25,基於標的股票的6月100買權的價格為4.65,6月110買權的價格為1.54。為了構造Gamma中性的空頭買權比率價差組合,假定做多1份6月100買權,同時做空x份6月110買權,則有:Gamma1+x·Gamma2=0;0.0326+x·0.0247=0得:x=-1.32
也就是說,要實現Gamma中性,要做多1份6月100買權,同時做空1.32份6月110買權。但通過這一比例
構造的空頭買權比率價差組合不能保證Delta中性。事實上,該組合的Delta值為:0.508-1.32·0.229=0.206如何保持新的組合為Delta中性(或近似中性)注意到相同執行價格的買權與賣權的Gamma值相等,因此,可以通過分解做多1份6月100買權為做多y份6月100買權,同時做多(1-y)6月100賣權來達到Delta中性,而又不影響原組合的Gamma中性。要求y的值,只要解如下簡
單方程:
0.508y-0.229×1.32+(-0.492)(1-y)=0
解得,y≈0.79
 風險中性
風險中性也就是說,通過如下操作:做多0.79份6月100買權;做空1.32份6月110買權;做多0.21份6月100賣權。
就能構造既為Delta中性,又為Gamma中性的組合。重新觀察各組合的敏感性參數,對比上述三種組合,發現,第三種組合確實實現了Delta與Gamma中性,進一步觀察各組合價值受標的股票價格變動的影響情況,
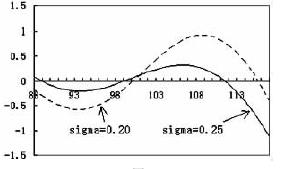
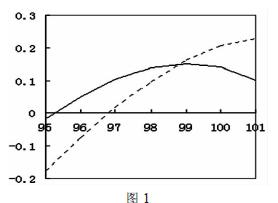
相對於組合1和組合2,組合3最為平坦,表明通過構造Delta及Delta-Gamma中性後,組合受價格波動的影響足夠小。由於事先賣出的期權份數多於買入的份數,上述組合屬於賣出波動率策略。希望未來波動率較構造組合時會下降。如果行情的發展確如預期的那樣,比如,sigma由構建組合時的0.25下降為0.20,則便可實現利潤。自構造組合一個月後,波動率保持不變與下降後組合價值的6月100買權(c1)6月110買權(c2)組合1(1c1:-2c2)組合2(1c1:-2.22c2)
實線代表波動率保持在0.25時組合的價值,虛線代表波動率降為0.20時組合的價值,發現,如果價格波動位於當初構造組合時所希望(預期)的波動範圍[100~110]內(即兩個不同的執行價格範圍內),投資者將會因為波動率的下降而實現套利。當然,這種套利要滿足一定的條件,一是到期標的股票價格的波動要落在執行價格的範圍內,二是波動率要如所預期的那樣呈下降趨勢。因此這種套利不是無風險的,這也是稱其為風險套利的原因。但從構造組合的過程來看,這種組合是Delta和Gamma中性,且theta的值也很小,表明時間的流逝對組合價值的影響也是很小的。因此,風險要較一般的1:2組合及僅僅為Delta中性組合的風險要小得多。

