關於極限
在點集拓撲學中也有與極限相似的概念,叫做極限點。從字面上看,極限點是極限就要到達的那一點。有時所說極限是數列或函式的極限,是變動的數的極限,極限過程是變數。有時所說極限是點列或映象的極限,是變動的點的極限,極限過程是動點。
度量空間點列
定義1
 極限點
極限點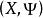 極限點
極限點 極限點
極限點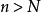 極限點
極限點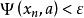 極限點
極限點 極限點
極限點設 是度量空間 的無限點列,a是常數,不管給定的正數 多么小,總存在N>0,當 , ,則稱a是無限點列 的一個極限點。
定義2
 極限點
極限點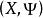 極限點
極限點 極限點
極限點 極限點
極限點 極限點
極限點設 是度量空間 的無限點列,a是 的一個極限點。則稱無限點列 收斂於a或極限為a,記為 。
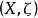 極限點
極限點例1 無限恆常數列 的極限點或極限均是x。
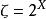 極限點
極限點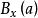 極限點
極限點 極限點
極限點 極限點
極限點 極限點
極限點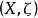 極限點
極限點例2設 是離散拓撲空問, ,任意x∈X, 是含x的開球,若要點列 收斂於x,則含x的開球必須包含 幾乎所有的項,之後的項均為X,從而 。
註記1:度量空間點列的極限點或極限是唯一的,但在非度量拓撲空間中,極限點或極限就不一定唯一。請看例3。
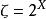 極限點
極限點 極限點
極限點 極限點
極限點 極限點
極限點例3設 是平凡拓撲空間,任意點x∈X,若 是X中的點列,則因為 中只有一個非空集X,所以包含x的球只有X,從而點列 收斂於X的任一點x。
極限點的定義
定義3
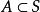 極限點
極限點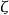 極限點
極限點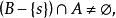 極限點
極限點設 是拓撲空間,,若對每個 中的集合B,s∈B,有
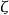 極限點
極限點則稱s是A的一個極限點。
註記2:定義3是在非度量拓撲空間中極限點的定義,它比定義1和定義2更廣泛,一般不具唯一性。
定理1
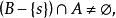 極限點
極限點 極限點
極限點設X是非空集, 是平凡拓撲.即 ,則以下3個結論成立:
(1)若A是空集,則A無極限點;
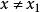 極限點
極限點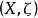 極限點
極限點(2)若A是單點集,其元素為 ,則只要 ,x都是A的極限點;
(3)若A至少有2個元素,則A中每一點都是A的極限點。
雙核拓撲會計
在雙核拓撲會計空間中所有的點都不是極限點,原因是以下定理。
定理2
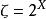 極限點
極限點 極限點
極限點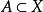 極限點
極限點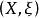 極限點
極限點設 是離散拓撲空間, 。則 不可能是任何 的極限點。
定理3
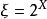 極限點
極限點 極限點
極限點雙核拓撲會計空間資產核 中,若 ,則所有資產核綱目都不存在極限點。
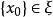 極限點
極限點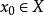 極限點
極限點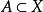 極限點
極限點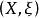 極限點
極限點證明 是X的所有子集的系,即 ,由定理2,任何 不可能是任何綱目 的極限點。
定理4
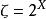 極限點
極限點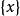 極限點
極限點雙核拓撲會計空間權益核 中,若 ,則所有權益核綱目都不存在極限點。
證明 同定理3的證明。
註記3:雙核拓撲會計空間Z沒有極限點,是因為我們為雙核會計空間選用了離散拓撲結構,由定理2.任何在單點集 中的點x都不可能是任何Z中的子集的極限點。
註記4:若我們為雙核會計空間選用平凡拓撲結構,則由定理1,空間每一點都是至少有兩個元素的集合的極限點,但是平凡拓撲結構太粗,不適合雙核會計空間。