證明
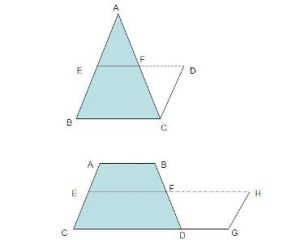
梯形中位線定理證明如圖，四邊形ABCD是梯形，AD∥BC，E、F分別是AB、CD邊上的中點，求證：EF∥AD，且EF=（AD+BC）/2
證明：
連線AF並延長交BC的延長線於G。
∵AD∥BC
∴∠ADF=∠GCF
∵F是CD的中點
∴DF=FC
∵∠AFD=∠CFG
∴△ADF≌△GCF(ASA)
∴AF=FG，AD=CG
∴F是AG的中點
∵E是AB的中點
∴EF是△ABG的中位線
∴EF∥BG,EF=BG/2=(BC+CG)/2
∴EF=(AD+BC)/2
∵AD∥BC
∴EF∥AD∥BC
特例做法
梯形中位線定理如圖的梯子。已知梯子每跨一步上升高度
相同，則求內部橫桿總長。
題示（做這些題目要注意題目的細節——上升高度相同，即每條橫桿都是小梯形的中位線）
如果同學沒有掌握技巧，只會死算，那么大多只能做如圖的最左的五步梯，可以設未知數解，時間消耗很大，尤其是運氣不佳遇到中間或右邊的多步梯，X、Y、Z算的都要吐血了。
但是題目做多了，我總結了一個規律，以左圖五步梯為例：五根橫桿的總長為1/2（30cm+50cm）X5
中圖七步梯為例：1/2(40cm+60cm)X7 那么同理，右圖九步梯則是1/2(50cm+70cm)X9
總結一下就是1/2(上底+下底)Xn
