簡介
有序無序轉變從物質結構上可區分為三種主要類型:①位置有序;②取向有序;③與電子自鏇及粒子自鏇狀態有關的有序等(見固態相變)。
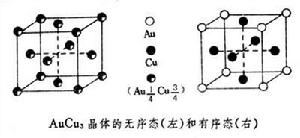
冶金工作者的注意力集中於位置有序無序轉變。許多固溶體在高溫時,溶質與溶劑原子在點陣中的分布是隨機的,而在低溫時溶質原子與溶劑原子卻分別位於某些特定位置上,這種現象稱為有序化或由無序到有序的轉變。其開始發生有序化的溫度稱為有序化溫度或有序化的臨界點。有序化以後的固溶體稱為有序固溶體,或稱超點陣(見合金相)。固溶體有序化之後,點陣的對稱性有所降低,或陣點的數目減少(如面心立方點陣變為簡單立方點陣),或點陣常數加大,這都會有附加的X射線衍射峰,這被稱為超點陣線條(圖1);超點陣一詞即由此得名。遠在1923年之前,塔曼(G.H.J.A.Tammann)已考慮到有序化的可能性,然而用X射線衍射的超點陣線條證實固溶體的有序化,卻是1923年由貝茵(E.C.Bain)以及1925年由尤安森(C.H.Johansson)和林德(J.O.Linde)發現的。
 有序無序轉變
有序無序轉變超點陣亦稱長程式。早已證實,在有序化溫度Tc以上,當長程式不復存在之後,在幾個原子間距的範圍內,原子的最近鄰、次近鄰及次次近鄰仍可保持有序狀態,這種小範圍的有序稱為短程有序或短程式。
多數有序無序轉變為連續的、協力型的二級相變,沒有潛熱效應。其中一部分為“λ相變”。這種協力型的相變特點是過程所需能量隨著過程進行程度的增加而減少,例如由有序變成無序,無序化所需能量隨無序程度的增加而遞減,即在過程接近完成時,其所需能量趨近於零。也有少部分有序無序轉變為一級相變,是不連續的,有潛熱效應。有些有序無序轉變既含有協力型的部分又具有不連續性部分。產生原子位置排列有序的驅動力涉及三個主要方面:①異類原子對之間的相互作用能。當以異類原子為鄰時,系統能量降低。②應力鬆弛。固溶體由不同大小的原子組成,有序化可降低應變能。③電子與布里淵區的相互作用。通過電子的費密面與有序結構的布里淵區的相互作用,導電電子的能量降低。多數有關有序化的工作是根據第一種假定進行的。
幾種常見的有序結構表1列出了一些合金的有序結構,這些常見結構是:L10、L12、B2、DO3、DO19、及L21(晶體結構報告符號),其中一個典型晶胞示於圖2中。
 有序無序轉變
有序無序轉變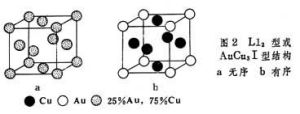 有序無序轉變
有序無序轉變有序疇(反相疇)及疇界有序結構被加熱到Tc溫度以上,將變成無序結構,但幾個原子間距範圍內的局部有序區仍然存在。當冷卻時,合金的有序化是以這些短程式區的獨立生長進行的,這些獨立生長的有序區稱有序疇,當這些不同地區的有序疇相遇時,如有相差,便形成明確的邊界,稱為疇界,亦稱反相疇界,因相鄰有序疇中的原子排列恰好反相。反相疇及疇界可用電子顯微鏡對薄晶體進行直接觀察,不同的有序結構顯示出不同形狀的疇界,圖3為AuCu3I(L12)型,有序結構中的有序疇及疇界的形狀。
 有序無序轉變
有序無序轉變另一種反相疇則是通過有序結構中的位錯運動造成的,一對這樣的位錯稱為超位錯,超位錯之間的區域即為反相疇。
有序度(有序參數)為了說明有序結構的有序程度引入有序度(或有序參數)的概念。以體心立方(CsCl)結構的CuZn為例,將這種點陣劃分為兩個簡單亞點陣,一個亞點陣由角隅上的原子構成,稱為α亞點陣,另一個由體心原子構成,稱為β亞點陣,當全部銅原子位於α亞點陣,全部鋅原子位於β亞點陣時則為完全有序,當50%的銅原子與鋅原子更換位置,即50%銅原子占在“正確”位置上,50%的銅原子占在“錯誤”位置上(鋅原子必隨之亦然),此時為完全無序,當完全有序時的序參數為1,完全無序時的序參數為0,由此將有序度ζ定義為:
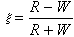 (1)
(1)
對AB型合金,R代表A原子占在“正確”位置上的數目,W代表A原子占在“錯誤”位置上的數目,顯然R+W=N為 A原子的總數。當R=W時,ξ=0,當R=N,W=0時,ξ=1。ξ 的數值是根據在整個點陣中計算“正確”位置上的原子數與“錯誤”位置上的原子數各自統計平均值得到的,它和正確原子與錯誤原子之間的距離無關。將這種序參數稱為長程式參數。
相似地,可以定義短程式參數。在 AB 型體心立方(bcc)結構的合金中,完全有序時A原子的最近鄰皆為B原子,B原子的最近鄰皆為A原子。若R1及W1分別代表正確最近鄰與錯誤最近鄰的數目,則短程式參數定義為:
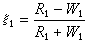 (2)
(2)
式中R1+W1=ZN,Z代表這種結構的配位數,即最近鄰原子數目,同樣可定義ξ2、ξ3作為次近鄰及次次近鄰的近程式參數。
長程式參數與X射線衍射超點陣線條強度I之間存在一定的定量關係:
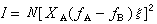 (3)
(3)
其中XA為合金中A原子的原子分數;fA、fB分別為A及B的散射因子。適當選擇X射線的波長,由超點陣線條的強度可測得 ξ。短程式參數 ξ1可由X射線的漫散強度測得。對一定成分的合金,其序參數隨溫度而改變,ξ與溫度的關係示於圖4。
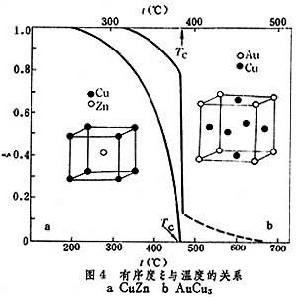 有序無序轉變
有序無序轉變處理有序無序轉變的近似方法處理有序無序轉變的近似方法已有很長的歷史。有布喇格 (Bragg)和威廉斯(Williams)近似法,簡稱(B-W)近似法,貝特(Bethe)法及準化學法等。
(B-W)近似法 這個方法的基本思路是由外斯(Wei-ss)處理鐵磁-順磁轉變的方法移植過來的。以 AB型合金為例,A、B原子各為N/2,合金的長程式參數為ξ,經推導,得
ξ=th(2Tcξ /T) (4)ξ 隨T/Tc的增大而連續下降。
Bethe模型 貝特(Bethe)考慮到次近鄰對最近鄰原子的影響,得到了比(B-W)近似法更好的結果,圖5表示以A為中心的兩層原子,它有Z個最近鄰原子(圖中為 4個),中心原子可能為一“正確”原子,亦可能為一“錯誤”原子,中心原子與其最近鄰原子相互作用,而這些最近鄰原子又與其外層的原子相互作用,而這種作用反過來又影響它們與中心原子的相互作用,這種附加的相互作用會影響第一近鄰原子類型出現的幾率,這一點在B-W的方法中是未加考慮的,因此將B-W近似稱為零級近似,而將Bethe方法稱為一級近似 (考慮一層)或二級近似(考慮兩層)。Bethe方法得到的有序化溫度較B-W方法為低,並可推知,在Tc以上仍有短程式存在;這兩個結論比B-W法所得結論,與實驗結果更為接近。
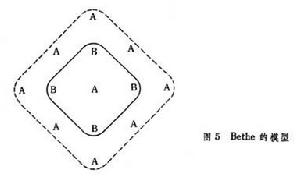 有序無序轉變
有序無序轉變準化學方法 最近鄰鍵模型的發展是以計算各種鍵的數目與隨機分布時相應鍵數的偏離情況來說明有序度。將有序轉變與化學反應相類比,計算A-A、B-B、A-B的濃度及其隨溫度的變化。
其他類型的有序無序轉變液晶是取自有序的一個例子,液晶的分子排列是長程無序的,在某一溫度以下,它的分子軸的空間取向發生長程有序化現象。磁性是磁矩發生長程有序的現象。磁性有序又可區分為鐵磁有序、逆鐵磁有序及亞鐵磁有序等。在鐵電、反鐵電材料中又可出現電矩的方向長程有序現象。在超導材料中會出現能隙有序的現象。這些有序現象與許多功能材料的性質有關。
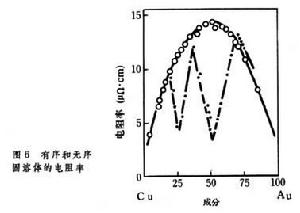
有序無序轉變引起的合金性能變化及套用 伴隨有序無序轉變,合金的某些物理的、力學的、化學的性質發生相應的變化。例如,合金的熱容量、電阻率、磁導率、硬度及屈服強度、彈性模量以及電極電勢等都會發生改變,其中熱容量和電阻率的變化是一個普遍現象,而其他性質變化的顯著程度要根據具體的合金系統而定。圖6為Cu-Au系有序固溶體與無序固溶體的電阻率,有序化引起合金的電阻率強烈降低。圖7示出有序化時的熱容量突變,其中圖7a變化是無限的,即為λ相變;圖7b變化是有限的。
 有序無序轉變
有序無序轉變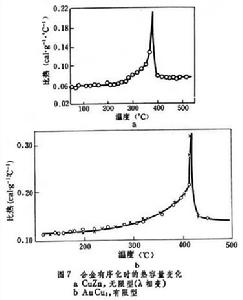 有序無序轉變
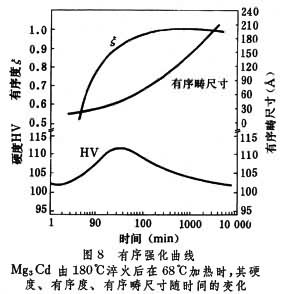
有序無序轉變有序無序轉變,是熱處理所依賴的固態相變之一。Ni3Mn在無序狀態是順磁的合金,有序化之後則為鐵磁性合金。以Cu2MnAl為代表的Heusler合金,儘管構成合金的各組元皆非鐵磁性元素,但當它呈現有序結構時顯示出很強的鐵磁性。另一類Heusler合金(Cu2NiAl,Zn2CuAu),其有序結構的晶體在一定溫度範圍中會出現熱彈性馬氏體相變,可作為形狀記憶合金。有些合金的有序化是與其脆性相聯繫的,Fe-Si合金中出現 DO3型的有序結構(Fe3Si)會引起合金的脆性。此外,通過適當的熱處理工藝控制有序疇的尺寸可獲得最佳的強化效果,稱為有序強化,見圖8。
 有序無序轉變
有序無序轉變參考書目
C.S.Barrett,T.B.Massaloki,Structure of Metals,3rd ed.,McGraw-Hill,New York,1980.
C.N.R.Rao,K.J.Rao,Phase Transition in Solids,McGraw-Hill,New York,1978.

