原理
有序度(有序參數) 為了說明有序結構的有序程度引入有序度(或有序參數)的概念。以體心立方(CsCl)結構的CuZn為例,將這種點陣劃分為兩個簡單亞點陣,一個亞點陣由角隅上的原子構成,稱為α亞點陣,另一個由體心原子構成,稱為β亞點陣,當全部銅原子位於α亞點陣,全部鋅原子位於β亞點陣時則為完全有序,當50%的銅原子與鋅原子更換位置,即50%銅原子占在‘’正確”位置上,50%的銅原子占在‘’錯誤”位置上(鋅原子必隨之亦然),此時為完全無序,當完全有序時的序參數為1,完全無序時的序參數為0。
位錯網路中反相疇界能與超位錯分解
由螺型超位錯組成的位錯網路中,螺型超位錯的分解寬度明顯大於單獨螺型超位錯的分解寬度。各向同性線性彈性理論計算表明,這一現象是由於位錯網路中,部分反相疇界相互抵消所致。隨著反相疇界能的減小,這一效應將變得更加顯著。
超位錯反應
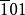 超位錯
超位錯 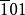 超位錯
超位錯 以中溫蠕變形變後的NiAl為試樣,用電子顯微學方法觀察到以下位錯反應和超位錯網路是一張g/3g弱束暗場像,示出了NiAl在580℃,400MPa蠕變10h後觀察到的超位錯反應。其中A和B是在不同{111}面上滑移的兩個螺型超位錯。它們的Burgers矢量分別為[101]和[]。並且,每一個超位錯分解為Burgers矢量為二分之一小於101大於的不全位錯,加上一個在(010)面上的反相疇界。在這裡,雖然兩個超位錯的Burgers矢量相互垂直,但是它們都分解在同一個立方面(010)上。當位錯反應發生後,形成一個‘’位錯結”,在這個‘’位錯結”內,由於兩個反相疇界相互重疊,其中一個具有位移矢量二分之一[101],另一個具有位移矢量二分之一[]。因此,它們重疊後,形成一個完整的晶格位移[001],即:在‘’位錯結”內,由於反相疇界相互抵消,一個‘’完整”的區域被恢復。
超位錯網路
位錯發生反應形成一個單獨的‘’位錯結”時,並不影響整個位錯的分解。但如果形成一系列的 ‘’位錯結”,即位錯網路,這時每個超位錯的分解明顯變寬。NiAl在580℃,400MPa蠕變20小時後拍攝到的一張超位錯網路的弱束照片。從這個超位錯網路的具體結構可見,它是由兩組相互垂直的螺型超位錯構成,每一超位錯分解為二分之一小於101大於的不全位錯。每一個長方形的區域表示反相疇界,每一個小正方形區域是反相疇界相互重疊抵消的區域。在超位錯網路中,超位錯的分解寬度明顯大於單獨位錯的分解寬度。
超位錯芯對單晶體臨界切應力的影響
通過對COTi單晶體的塑性變形研究,揭示COTi的強度隨溫度呈複雜變化的特性,尤其是隨溫度升高時它所表現出的高強度,對發展耐熱合金有很大意義。
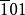 超位錯
超位錯 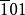 超位錯
超位錯 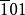 超位錯
超位錯 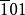 超位錯
超位錯 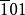 超位錯
超位錯 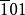 超位錯
超位錯 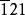 超位錯
超位錯 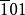 超位錯
超位錯 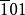 超位錯
超位錯 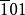 超位錯
超位錯 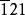 超位錯
超位錯 能夠較成功地解釋強度隨溫度升高而增強現象的理論是Kear一一Wilsdorf的螺位錯交滑移系模式,在L12型 晶體結構中,a[101]超位錯分解為二個1/2a[01]分位錯,其間夾反向疇界。由於在(111)面上的反向疇界能很大 (最近鄰原子對發生錯位),而在(010)面上的反向疇界能很小 (最近鄰原子對不發生錯位) 。因此,(111)面上的a[]超位錯趨於向(010) 面上交滑移,其驅動力為(111) 面上的反向疇界能與(010)面上的反向疇界能之差,最近Y00提出晶體的各向異性也可成為此種交滑移的驅動力。產生交滑移的部分對在(111) 面上運動的a[]螺位錯起阻礙做用。1973年竹內藏元指出螺位錯的這種交滑移是熱激活過程,溫度越高,交滑移的趨向越大 。指出在(010)[]滑移系的分切應力將促進這種交滑移。因此定義了參數N,N為 (010)[]滑移系的斯密特因子與(111)[101]滑移系的斯密特因子之比。N值越大交滑移的趨向越大,(111)[]滑移系的臨界切應力越大。1979年Lall等人提出當(111)面上的1/2a[]分位錯分解為二個1/6a []型不全位錯時,必需首先束集為1/2a[]分位錯,然後才能交滑移。在束集過程中,(111)[121]滑移繫上的分切應力將起促進作用。為表征上述效果(111)[]滑移系的斯密特因子與(111)[]滑移系的斯密特因子 之比定義為Q值,Q值越大,交滑移的趨向越大 。當變形方向反向時,兩個1/6a[]型不全位錯所受的作用力亦反向。因此Q可取正值或負值。

