固體中的元激發
正文
固體中某種振動或波的能量量子。固體物理中的元激發或準粒子的概念和粒子物理中的“物理”粒子或重正化了的粒子的概念相似。在固體這樣一種有複雜相互作用的多體系統中，常常有一些激發態的性狀可以近似地類比於一些自由粒子，雖然這些激發態是有相當複雜內在結構的集體狀態。元激發與準粒子 聲子也許是一個最為人們熟知的例子。固體的原子之間有強的相互作用，每個原子都只能在陣點附近作微小振動，每個原子的運動都要牽動周圍的原子，以點陣波的形式在晶體中傳播。在簡諧近似下，點陣振動可以看作是一系列相互獨立的簡諧振動的疊加，每種簡諧振動對應於一種點陣波，有自己的頻率和波矢，它的能量變化是量子化的，能量量子叫做聲子（見點陣動力學）。聲子具有能量啚ω（啚是普朗克常數除以2π,ω 是相應點陣波頻率），和準動量啚k（k是相應點陣波的波矢）。但波矢只定義在第一布里淵區內，準動量守恆也只準確到可以相差一個倒易點陣矢量。聲子是一種玻色子，遵從玻色統計。由於每種簡振模式可以處於任意激發態，所以聲子的數目是不確定的。只要非諧作用不很強，也可以把非諧作用用引入聲子之間的相互作用來描寫（見非諧相互作用）。這樣一來，通過引入簡正坐標──點陣波模式，相互作用的原子系統的小振動，即這個系統的低激發態，可以近似看作是一個沒有相互作用(或只有弱的相互作用)的準粒子──聲子──的系統。這個相互作用的原子系統的熱力學性質和近於平衡的某些非平衡過程都可以用聲子系統的熱力學和輸運過程來討論。
金屬中的電子氣也是一個有很強的相互作用的多粒子系統。一個運動著的單電子，由於泡利不相容原理和靜電庫侖作用，要排斥周圍的負電荷──電子，因而其周圍就好像裹上一層正電荷的“雲”。正電荷雲禁止了該電子和其他電子間的庫侖作用,使電子-電子間的作用從長程的庫侖作用變成短程的禁止庫侖作用。同時，這團裹在外面的正電荷雲修正了單電子的有效質量。這種由電子和相隨的正電荷雲組成的複合體稱為準電子。如果考慮禁止庫侖作用引起的散射,準電子有一定壽命;對動量離費密面較遠的準電子，壽命太短，使準電子的概念失去意義。因此，對相互作用的電子氣，近於基態的激發態中，有一種可以近似看作是近獨立的單粒子型的激發──準電子，它遵守費密統計。
除此以外，在相互作用的電子氣中還會有另一類型的集體激發：考慮一個進入電子氣中的電子，它排斥的負電荷──電子──會被剩下的正電荷吸引，這會導致正負電荷的往返振盪。這種振盪其實是電子氣相對於固定的正離子背景的集體振盪，它是以波的形式傳播的。波矢為零（即波長為無窮大）的這種集體振盪的頻率是
其中n是電子氣的密度，e是電子電荷，m是電子質量，ε是媒質的介電常數。這種振盪稱電漿振盪，類似於前述的點陣振動，它的能量也是量子化的,等於媡ωp（ωp是它的振盪頻率）,這個振盪量子叫做等離激元；它也是一種玻色子。如果進入電子氣的電子有足夠的能量，就可以激發出這種準粒子。 準粒子的相互作用和固體的性質 各類準粒子之間也會有相互作用。金屬中的電子不僅排斥其他電子,還會吸引周圍的正離子，正離子的位移可以表示為點陣簡正坐標的疊加,這便是電子和聲子的耦合。這種耦合也要改變運動電子的有效質量。這樣考慮的電子就不僅是電子和周圍正電荷的複合體，而是它們和伴隨的點陣的極化的複合體,但在電子能量不太高時,它還可看作是一個準電子。考慮電子-聲子的耦合,不僅會改變準電子的內容與參量,而且還會改變準電子之間的相互作用。一對電子之間可通過交換聲子而進行能量和動量的傳遞，已經證明，對金屬來說,在費密面附近一薄層內的電子,這種作用是吸引作用。如果這種交換聲子而產生的吸引作用,超過電子間的禁止庫侖作用，則費密面附近的電子之間便是互相吸引的。在這種情況下多粒子系統的單粒子激發譜會發生本質的變化。因為在費密面附近一對吸引的粒子會形成束縛態，或更確切一些說，吸引作用會導致粒子系統的負的相關能，結果這部分在費密面附近一薄層內的電子的能量要比正常態的低，我們稱這部分電子為凝聚相。從凝聚相激發一個動量為p 的單粒子，所需的激發能不再是原來的
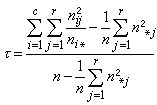(m*是前面所述的準電子有效質量,是費密能量)，而是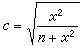
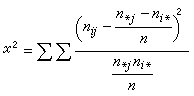。所以,如果激發的電子的動量是費密動量,激發能量也不是零,而是墹。這樣單粒子激發的能譜就和前述準電子的能譜有本質不同：在基態與單粒子激發態之間出現能隙墹。在這個情況下，系統成為超導相(見超導電性、超導微觀理論)。超導態的單粒子激發譜是溫度的函式，溫度升高就有更多的凝聚相里的粒子激發為準粒子，凝聚相相關能隨之減小，到某個臨界溫度Tc時,能隙墹減小到零，單粒子激發譜E(p)又變回到通常的準電子能譜。顯然,超導態的準粒子數目並不守恆。以上一些例子告訴我們,作為多體系統的集體運動的一種模式的準粒子，不僅其能量-動量關係可能與平常的粒子不同,而且有時也可以沒有粒子數守恆的要求。 金屬中電子氣體的各類元激發的概念是在Л.Д.朗道提出的正常費密液體基礎上發展起來的。朗道理論普遍說明了低溫下一個相互作用費密粒子系統的性狀，可以用一些只有弱相互作用的準粒子系統的性狀來表達。這不僅為理解金屬性質提供了理論基礎;而且對研究3He的量子流體性質，甚至對研究重原子核的特性和認識某些天體的特性都起了重要影響。
元激發的概念對理解半導體和絕緣體的性質也很重要。在有離子性的半導體中，載流子對正負離子的作用是相反的，結果形成圍繞它的點陣的電極化場，這實質上是電子和光頻支聲子的耦合。這種耦合形成新的複合體， 稱作極化子。 它其實是在這種情況下的準電子。如果這個晶體是立方點陣，庫侖作用耦合的是縱向光頻支聲子。在弱耦合情形下，極化子的能量－動量關係是
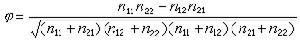；這裡，α是電子-聲子耦合常數，ωe是縱向光頻支聲子頻率，
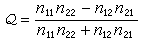m*是電子有效質量。α對許多晶體來源，並不是一個很小的數,例如對溴化鉀，α＝3.52，對砷化鎵，α＝0.06。由此可見，這修正還是必要的。 不僅對認識電子的運動，就從認識光波與晶體的相互作用來說，準粒子的概念也很重要。如果點陣振動能產生伴隨的電偶極矩，光波與這個電偶極矩的作用實質上便是光子與某幾支聲子的耦合，這引起點陣對光的吸收與色散現象。假如某一支光頻聲子能和光耦合，它的色散關係（即這支聲子的頻率-波矢關係）是ω(k)。已經知道光子的色散關係是ω＝ck，c是光速，k是光波波數。那么,對於滿足方程ω(k)=ck的波矢ko附近的點陣波來說，它和光波的耦合由於兩者的頻率與波矢都近於相等，而變得很強；這時就形成一種新的激發模式，它其實是點陣波與光波的耦合波，對應的元激發稱極化激元。這是黃昆在1950年首先提出的。
假如光波的頻率近於或大于禁頻寬度，在晶體中它就會產生電子和空穴。但帶負電荷的電子與帶正電荷的空穴之間有庫侖吸引作用,它們會組成電子-空穴對的束縛態,就好像一個氫原子一樣。這種束縛態稱作激子,它是電中性的，在晶體中傳輸時將不能運載電流，但可以運載能量。激子有自己的質心動量和質心動能，相當於一個質量為me+mh的粒子（me是電子有效質量，mh是空穴有效質量）。束縛態能量是一些分立的值，激子對光的吸收表現為在帶間吸收邊下面的一些吸收峰。
在了解鐵磁性、反鐵磁性或亞鐵磁性時，另一種元激發──磁振子或自鏇波量子的概念也是常用的。作為例子考慮一個簡單的鐵磁系統，它的基態全部自鏇是平行的。如果有任何一個自鏇倒向，由於和相鄰自鏇的交換作用，這會引起周圍自鏇的進動，而以波的形式傳播。這種波稱為自鏇波。類似於點陣振動，自鏇波的能量也是量子化的，能量量子稱磁振子。它也是一種玻色子。根據磁振子和電磁波的相互作用,對中子的散射等等,可以從實驗上測量磁振子的能量-動量關係。
從上面所舉的這些元激發的例子，可以看出元激發概念在固體物理中的作用。對一個相互作用的多體系統，它的低激發態的性狀等等可歸結為一支或幾支近獨立的元激發,它們是許多粒子集體的一些穩定的激髮狀態,在空間上可能是非局域的;它們各有自己的能量和動量,而且能量和動量的關係可以不同於通常的粒子；它們的數目也可以是不守恆的，各自服從不同的統計。可以這樣來理解；假使一定的能量和動量注入系統，並且能量動量滿足某種色散律；如果它可以被系統吸收，激發起一種穩定的激發,那就是說系統中產生了一種元激發,或者說一種準粒子，它的能量動量關係就是上述色散律。但是，必須注意，準粒子的概念只有在它們之間的相互作用以及它們和其他粒子或物理因素的相互作用比較弱時才有意義。以聲子為例，如果非諧作用比較強，或溫度比較高，聲子之間的散射很頻繁，以致於聲子的壽命已近於它的頻率的倒數（即它的振動周期），這時再使用聲子的概念就不合適了。
