簡介
根據閉環控制系統的開環頻率回響判斷閉環系統穩定性的準則,美國學者H.奈奎斯特1932年所提出。控制系統在斷開反饋作用後所定出的頻率回響稱為開環頻率回響。奈奎斯特穩定判據本質上是一種圖解分析方法,且開環頻率回響容易通過計算或實驗途徑定出,所以它在套用上非常方便和直觀。奈奎斯特穩定判據只能用於線性定常系統。在經典控制理論中,奈奎斯特穩定判據主要用於分析單變數系統的穩定性。在此基礎上形成的頻率回響法是經典控制理論的主要分析和綜合方法之一。70年代以來,奈奎斯特穩定判據已被推廣套用於多變數系統(見多變數頻域方法)。
基本形式
 奈奎斯特穩定判據
奈奎斯特穩定判據推廣形式
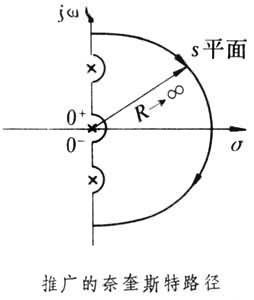
當開環傳遞函式G(s)在s複數平面的虛軸上存在極點或零點時,必須採用判據的推廣形式才能對閉環系統穩定性作出正確的判斷。在推廣形式判據中,開環頻率回響G(j&owega;)的奈奎斯特圖不是按&owega;連續地由 0變到∞來得到的,&owega;的變化路徑如圖所示,稱為推廣的奈奎斯特路徑。在這個路徑中,當遇到位於虛軸上G(s)的極點(圖中用×表示)時,要用半徑很小的半圓從右側繞過。只要按這條路徑來作出G(j&owega;)從&owega;=0變化到&owega;=∞時的奈奎斯特圖,則Z=P-2N和關於穩定性的結論仍然成立。
回響穩定
這種判據在實質上與奈奎斯特判據相似。惟一的差別在於,對數判據是根據 G(j&owega;)的幅值對數圖和相角圖來確定N的。在幅值對數圖上特性為正值時的頻率區間內,規定相角圖上特性曲線由下向上穿過-180°線稱為正穿越,而由上向下稱為負穿越。分別用N+ 和N- 表示正穿越次數和負穿越次數,則N=N+ -N- 。判據的結論仍然是Z=P-2N,且Z=0時閉環系統穩定,Z≠0時閉環系統不穩定。由於頻率回響的幅值對數圖和相角圖易於繪製,因此對數頻率回響穩定判據套用更廣。