思想
《九章算術》是中國古代的數學專著,其中的“更相減損術”可以用來求兩個數的最大公約數,原文是:
白話文譯文:
(如果需要對分數進行約分,那么)可以折半的話,就折半(也就是用2來約分)。如果不可以折半的話,那么就比較分母和分子的大小,用大數減去小數,互相減來減去,一直到減數與差相等為止,用這個相等的數字來約分。
使用步驟
第一步:任意給定兩個正整數;判斷它們是否都是偶數。若是,則用2約簡;若不是則執行第二步。
第二步:以較大的數減較小的數,接著把所得的差與較小的數比較,並以大數減小數。繼續這個操作,直到所得的減數和差相等為止。
則第一步中約掉的若干個2與第二步中等數的乘積就是所求的最大公約數。
其中所說的“等數”,就是最大公約數。求“等數”的辦法是“更相減損”法。
實例
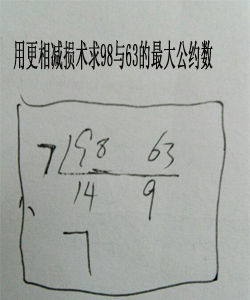
例1、用更相減損術求98與63的最大公約數。
解:由於63不是偶數,把98和63以大數減小數,並輾轉相減:
98-63=35
63-35=28
35-28=7
28-7=21
21-7=14
14-7=7
所以,98和63的最大公約數等於7。
例2、用更相減損術求260和104的最大公約數。
解:由於260和104均為偶數,首先用2約簡得到130和52,再用2約簡得到65和26。
此時65是奇數而26不是奇數,故把65和26輾轉相減:
65-26=39
39-26=13
26-13=13
所以,260與104的最大公約數等於13乘以第一步中約掉的兩個2,即13*2*2=52。
比較
輾轉相除法也可以可以用來求兩個數的最大公約數。
更相減損術和輾轉相除法的主要區別在於前者所使用的運算是“減”,後者是“除”。從算法思想上看,兩者並沒有本質上的區別,但是在計算過程中,如果遇到一個數很大,另一個數比較小的情況,可能要進行很多次減法才能達到一次除法的效果,從而使得算法的時間複雜度退化為O(N),其中N是原先的兩個數中較大的一個。相比之下,輾轉相除法的時間複雜度穩定於O(logN)。
Stein算法
更相減損法有點類似於求最大公約數的Stein算法。在更相減損法中,若兩個是偶數則同除以2,結果乘以2。如果增加一個判斷,若為一奇一偶則偶數除以2,結果不變,若為兩個奇數才相減,這樣就變成了目前計算大整數最大公約數的非常好的一個算法,Stein算法。
在上面的實例中,下面是更相減損法與Stein算法的比較,從中可以發現兩種算法的相似性。
| 更相減損法:操作 | 甲數 | 乙數 | Stein算法:操作 | 甲數 | 乙數 |
| 98 | 63 | 98 | 63 | ||
| 98-63=35 | 63 | 35 | 98是偶數,除以2 | 49 | 63 |
| 63-35=28 | 35 | 28 | 都是奇數,63-49=14 | 49 | 14 |
| 35-28=7 | 28 | 7 | 14是偶數,除以2 | 49 | 7 |
| 28-7=21 | 7 | 21 | 49-7=42 | 42 | 7 |
| 21-7=14 | 7 | 14 | 42是偶數,除以2 | 21 | 7 |
| 14-7=7 | 7 | 7 | 21-7=14 | 14 | 7 |
| 7-7=0 | 7 | 0 | 14是偶數,除以2 | 7 | 7 |
| 7-7=0 | 7 | 0 |
“可半者半之”
通常認為,算法描述中的第一步“可半者半之”是指分子分母皆為偶數的時候,首先用2約簡。因為更相減損術原先是專用來約分,所以並不用考慮最後計算結果時,要把第一步中約掉的若干個2再乘回去。加入這一步的原因可能是,分母、分子皆為偶數是在分數加減運算的結果中比較容易遇到的一種情況,用這種方法有可能減少數字的位數,簡化計算。
當然,省略這個以2約簡的步驟,也能得到正確的答案。
電腦
Basic
INPUT "m,n=";m,n
i=0
WHILE m MOD 2=0 AND n MOD 2=0
m=m/2
n=n/2
i=i+1
WEND
DO
IF m<n THEN
r=m
m=n
n=r
END IF
m=m-n
LOOP UNTIL m=0
PRINT “m、n的最大公約數為”;n*2ˆi
END
(黑體部分可以省略,因為,不進行約簡,一樣可以求出)
C語言
#include <stdio.h>
int main()
{
int a,b;
scanf("%d%d",&a,&b);
while(a != b)
{
if(a > b)
a -= b;
else
b -= a;
}
printf("m、n的最大公約數為%d",a);
return 0;
}