來源
 歐幾里德
歐幾里德設兩數為a、b(a>b),求a和b最大公約數(a,b)的步驟如下:用a除以b,得a÷b=qr(0≤r1)。若r=0,則(a,b)=b;若r≠0,則再用b除以r,得b÷r=qr(0≤r).若r=0,則(a,b)=r,若r≠0,則繼續用r除以r,如此下去,直到能整除為止。其最後一個為被除數的餘數的除數即為(a, b)。
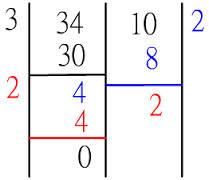
例如:a=25,b=15,a/b=110,b/10=15,10/5=20,最後一個為被除數餘數的除數就是5,5就是所求最大公約數。
原理
設兩數為a、b(b
第一步:令c=gcd(a,b),則設a=mc,b=nc
第二步:根據前提可知r =a-kb=mc-knc=(m-kn)c
第三步:根據第二步結果可知c也是r的因數
第四步:可以斷定m-kn與n互質【否則,可設m-kn=xd,n=yd (d>1),則m=kn+xd=kyd+xd=(ky+x)d,則a=mc=(ky+x)dc,b=nc=ycd,故a與b最大公約數成為cd,而非c,與前面結論矛盾】
從而可知gcd(b,r)=c,繼而gcd(a,b)=gcd(b,r)。
證畢。
算法
自然語言描述
用輾轉相除法確定兩個正整數 a 和 b(a≥b) 的最大公因數gcd(a,b):
當a mod b=0 時gcd(a,b)=b,否則
gcd(a,b) = gcd(b,a mod b)
遞歸或循環運算得出結果
偽代碼
這個算法可以用遞歸寫成如下:
function gcd(a,b) {
if b<>0
return gcd(b,a mod b);
else
return a;
}
gcd 簡易函式
c語言輾轉相除代碼:
int GCD(int a,int b)
{returnb==0?a:GCD(b,a%b);}
C語言實現
/*題目:輸入兩個正整數,求其最大公約數。*/
#include
unsigned gcd ( unsigned,unsigned ) ;
int main( void )
{
unsigned m,n;
printf("請輸入兩個正整數:");
scanf("%u%u",&m,&n);
printf("%u與%u的最大公約數為:%u\n",m,n,gcd ( m,n ) );
return 0;
}
/* 功能:返回正整數m和n的最大公約數*/
unsigned gcd ( unsigned m,unsigned n )
{
unsigned temp;
if (m
{
temp=m;
m=n;
n=temp;
}
if ( m % n == 0)
{
return n;
}
else
{
return gcd ( n,m % n) ;
}
}
/*題目:輸入兩個非負整數u和v,求其最大公約數。*/
#include
main()
{
int u,v,r;
printf("please input u and v:");
scanf("%d,%d",&u,&v);
while(v!=0)
{
r=u%v;
u=v;
v=r;
}
printf("%d\n",u);
}
C#語言實現
static int sucDivison/*除法*/(int m, int n)
{
int remainder = 0;
if (m % n == 0)
{
return n;
}
else
{
do
{
remainder = m % n;
m = n;
n = remainder;
} while (remainder > 0);
}
if (n == 0)
{
return m;
}
return n;
}
Basic實現
INPUT m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END
Pascal實現
function gcd(a,b:integer):integer;
begin
if b=0 then gcd:=a
else gcd:=gcd (b,a mod b);
end ;
Common Lisp實現
(defun my-gcd (number-a number-b)
(do ((r (mod number-a number-b) (mod ea eb))(eb number-b r) (ea number-a eb))
((= 0 r) eb)))
Java 實現
/**
*
* @return int
* @tags @param m
* @tags @param n
* @tags @return
* @todo 【方法二】利用輾除法
*/
public static int gcd(int m, int n) {
while (true) {
if ((m = m % n) == 0)
return n;
if ((n = n % m) == 0)
return m;
}
}
數據舉例
其中“a mod b”是指取 a ÷ b 的餘數。
例如,123456 和 7890 的最大公因子是 6,這可由下列步驟看出:
| a | b | a mod b |
| 123456 | 7890 | 5106 |
| 7890 | 5106 | 2784 |
| 5106 | 2784 | 2322 |
| 2784 | 2322 | 462 |
| 2322 | 462 | 12 |
| 462 | 12 | 6 |
| 12 | 6 | 0 |
時間複雜度
輾轉相除法的運算速度為 O(n),其中 n 為輸入數值的位數。
輾轉相除法處理大數時非常高效,它需要的步驟不會超過較小數的位數(十進制下)的五倍。加百利·拉梅(GabrielLamé)於1844年證明了這點,開創了計算複雜性理論。
套用
求不定方程的一組整數解方法
[註:以下出現的q,r括弧中的是下標,gcd(a,b)為a,b的最大公約數]
輾轉相除法可以求出特定條件的不定方程的一組整數解。
設不定方程為ax+by=c,其中a,b,c為整數,且 gcd(a,b) | c
a,b輾轉相除的算式為
b=q a+r
a=q r+r
r=q r+r
...
r=qr+r
r=qr
其中r=gcd(a,b),不妨令b=r,a=r,r=0
第i個算式為
r= q×r+ r
所以r= r - qr(i)(1)
用公式(1)可以得到r=gcd(a,b)關於a,b的線性組合sa+tb=gcd(a,b)
所以不定方程a×x+b×y=c的一組特解為x=s×c/gcd(a,b) y=t×c/gcd(a,b)
舉例說明
例如不定方程為326x+78y=4,求出一組整數解x,y
求(326,78)的算式為:
326=4*78+14
14=326-4*78
78=5*14+8
8=78-5*14
14=1*8+6
6=14-1*8
8=1*6+2
2=8-1*6
6=3*2
所以
2=8-6=8-(14-8)
=2*8-14=2*(78-5*14)-14
=2*78-11*14=2*78-11*(326-4*78)
=46*78-11*326
即2=(-11)*326+46*78
所以4=(-22)*326+92*78
所以x = - 22, y = 92是不定方程326x+78y=4的一組解。
相關原理
兩個整數的最大公約數是能夠同時整除它們的最大的正整數。
輾轉相除法基於如下原理:兩個整數的最大公約數等於其中較小的數和兩數的相除餘數的最大公約數。
例如,252和105的最大公約數是21(252 = 21 × 12;105 = 21 × 5);
因為252 ÷105 = 242,所以(105,42)是21。在這個過程中,較大的數縮小了,所以繼續進行同樣的計算可以不斷縮小這兩個數直至餘數變為零。這時的除數就是所求的兩個數的最大公約數。由輾轉相除法也可以推出,兩數的最大公約數可以用兩數的整數倍相加來表示,如21 = 5 × 105 + (−2) × 252。這個重要的等式叫做貝祖等式(又稱“裴蜀定理”)。