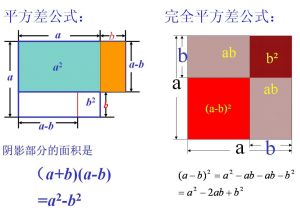
智慧數性質
比如:2^2-1^2=3,3就是智慧數。
命題
形如2k+1或4k的形式必為智慧數,智慧數的形式必為2k+1或4k的形式,k≥0。
以下給予推導證明:
令P=a^2 -b^2(P、a、b均為正整數)
1、若a=2m(m≥1),b=2n(n≥1)
則P=4m^2 -4n^2=4(m^2 -n^2),此時P為4k形式。
2、若a=2m(m≥1),b=2n+1(n≥0)
則P=4m^2 -4n^2-4n-1=4(m^2 -n^2 -n)-1,此時P為4k -1形式。
3、若a=2m+1(m≥1),b=2n(n≥1)
則P=4m^2+4m+1-4n^2=4(m^2+m- n^2)+1,此時P為4k+1形式。
4、若a=2m+1(m≥1),b=2n+1(n≥0)
則P=4m^2+4m+1-4n^2-4n-1=4(m^2+m- n^2-n),此時P為4k形式。
又易知4k -1,4k+1包括了所有的奇數,即(4k+1)∪(4k -1)=2k+1
故P為2k+1或4k的形式,即智慧數為2k+1或4k的形式
又2k+1=(k+1)^2 –k^2,
4k=(k+1)^2 –(k-1)^2
故形如2k+1或4k的形式必為智慧數。
5.驗證2687是否為智慧數
∵2687為奇數∴設2687=2k+1(k為正整數)
∴k=1343∴2687=1344²-1343²∴2687是智慧數
命題得證
自然數列中最小的智慧數是0,第2個智慧數是1,第3個智慧數是3,依次是0,1,3,4,5, 7, 8; 9, 11, 12; 13, 15, 16; 17, 19, 20······ 即按一個4的倍數,2個奇數,三個一組地依次排列下去。
像5^2-3^2=16,16就是智慧數。
公式
非智慧數:N/4+2
智慧數:N-(N/4+2)
第2012個智慧數
2012-1÷3+1×4+1=2685