普朗克尺度

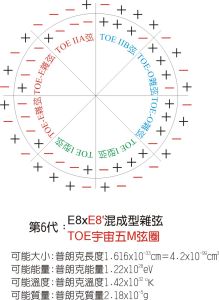
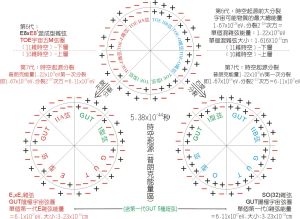
普朗克尺度-內部結構模型圖

經典廣義相對論的奇性不可避免，所以標準大爆炸模型中時空存在著零點，給了上帝一個容身之地。但是考慮到量子力學的測不準原理，一些基本量度，譬如長度和時間具有測不準性。測不準的程度由普朗克常數確定，從該常數可以定出最小的長度量子，即普朗克長度，為10E－33厘米，這遠遠小於原子核的尺度。測量任何長度不可能比這個更精確，而且比普朗克長度更短的長度是沒有意義的。同樣，作為時間量子的最小間隔，即普朗克時間，為10E－43秒。沒有比這更短的時間存在。這就是說，我們不可能把黑洞縮減為數學上的一個點，同樣也不能追溯到大爆炸的真正開始時刻。
普朗克長度l=gh/c3～10-35m=10E-33厘米
普朗克常數記為h，是一個物理常數，用以描述量子大小。在量子力學中占有重要的角色，馬克斯·普朗克在1900年研究物體熱輻射的規律時發現，只有假定電磁波的發射和吸收不是連續的，而是一份一份地進行的，計算的結果才能和試驗結果是相符。這樣的一份能量叫做能量子，每一份能量子等於普朗克常數乘以輻射電磁波的頻率。這關係稱為普朗克關係，用方程表示普朗克關係式，
E=hν；
其中，E是能量，h是普朗克常數，ν是頻率。
普朗克常數的值約為：
h=6.626\069\3(11)\times10^{-34}\\MBOX{J}\cdot\mbox{s}.
其中電子伏特（eV）·秒（s）為能量單位：
h=4.135\667\43(35)\\times10^{-15}\mbox{eV}\cdot\mbox{s}
普朗克常數的物理單位為能量乘上時間，也可視為動量乘上位移量：
（牛頓（N）·米（m）·秒（s））為角動量單位
另一個常用的量為約化普朗克常數（reducedPlanckconstant），有時稱為狄拉克常數(Diracconstant)，紀念保羅·狄拉克：
\hbar\equiv\FRAC{h}{2\pi}=1.054\571\68(18)\times10^{-34}\\mbox{J}\cdot\mbox{s},
其中π為圓周率常數pi。\hbar念為"h-bar"。
普朗克常數用以描述量子化，微觀下的粒子，例如電子及光子，在一確定的物理性質下具有一連續範圍內的可能數值。例如，一束具有固定頻率ν的光，其能量E可為：
E=nh\nu\,,\quadn\in\mathbb{N}
有時使用角頻率ω=2πν：
E=n\hbar\omega\,,\quadn\in\mathbb{N}
許多物理量可以量子化。例如角動量量子化。J為一個具有鏇轉不變數的系統全部的角動量，JZ為沿某特定方向上所測得的角動量。其值：
\begin{matrix}J^2=j(j+1)\hbar^2,&j=0,1/2,1,3/2,\ldots\\J_z=m\hbar,\qquad\quad&m=-j,-j+1,\ldots,j\end{matrix}
因此，\hbar可稱為"角動量量子"。
普朗克常數也使用於海森堡不確定原理。在位移測量上的不確定量（標準差）Δx，和同方向在動量測量上的不確定量Δp，有如下關係：
\Deltax\Deltap\ge\begin{matrix}\frac{1}{2}\end{matrix}\hbar
還有其他組物理測量量依循這樣的關係，例如能量和時間。