歷史起源
在100多年前的1900年,物理學家馬克斯•普朗克發現,能量可以分為不可再分割的單位,並將其命名為“量子”。為了描述量子的體積,人們通常使用基本量子即普朗克量子來形容。這一發現標誌著量子力學的誕生,其對科學發展起的作用超出普朗克本人的想像。例如,把普朗克量子同光速和其他常數結合在一起,就可以得出空間和時間方面不可分割的量子,也就是最短的距離單位和最短的時間單位。普朗克長度為10的-35次方米。普朗克時間為10的-43次方秒。
普朗克
如何超越普朗克長度和普朗克時間還是個謎,因為現行物理定律在這個範圍內就失效了。因此,宇宙論學者在研究宇宙起源時,在大爆炸之後,最多就能計算到10的-43次方秒。要研究普朗克時間之前發行的事,還缺乏新定律。這種新定律,理論物理學家已研究幾十年了。
經典廣義相對論的奇性不可避免,所以標準大爆炸模型中時空存在著零點,給了上帝一個容身之地。但是考慮到量子力學的測不準原理,一些基本量度,譬如長度和時間具有測不準性。測不準的程度由普朗克常數確定,從該常數可以定出最小的長度量子,即普朗克長度,為10E-33厘米,這遠遠小於原子核的尺度。測量任何長度不可能比這個更精確,而且比普朗克長度更短的長度是沒有意義的。同樣,作為時間量子的最小間隔,即普朗克時間,為10E-43秒。沒有比這更短的時間存在。這就是說,我們不可能把黑洞縮減為數學上的一個點,同樣也不能追溯到大爆炸的真正開始時刻。
運算
普朗克尺度,即HBAR,C,G都取為一時得到的時間,長度,質量尺度。
普朗克長度l=gh/c3~10-35m=10E-33厘米
普朗克常數也使用於海森堡不確定原理。在位移測量上的不確定量(標準差)Δx ,和同方向在動量測量上的不確定量 Δp,有如下關係:
原理
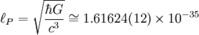 普朗克時間
普朗克時間普朗克長度lp計算如右圖,單位:米,普朗克時間為tp=lp/c= 5.39121(40) × 10^-44秒,
c為真空中光速,G為萬有引力常數(引力常量),G=6.67259×10^-11N.m^2/kg^2,普朗克常數記為 h ,是一個物理常數,用以描述量子大小。在量子力學中占有重要的角色,馬克斯·普朗克在1900年研究物體熱輻射的規律時發現,只有假定電磁波的發射和吸收不是連續的,而是一份一份地進行的,計算的結果才能
和試驗結果是相符。這樣的一份能量叫做能量子,每一份能量子等於hv,v為輻射電磁波的頻率,h為一常量,叫為普朗克常數。普朗克常數的值約為:
h=6.6260693(11)×10^-34 J·s,
或
h=4.13566743(35)×10^-15 eV·
其中電子伏特(eV)·秒(s)為能量單位:
普朗克常數的物理單位為能量乘上時間,也可視為動量乘上位移量:
(牛頓(N)·米(m)·秒(s))為角動量單位
另一個常用的量為約化普朗克常數(reduced Planck constant),有時稱為狄拉克常數(Dirac constant),紀念保羅·狄拉克:
其中 π 為圓周率常數 pi。 念為 "h-bar" 。
普朗克常數用以描述量子化,微觀下的粒子,例如電子及光子,在一確定的物理性質下具有一連續範圍內的可能數值。例如,一束具有固定頻率 ν 的光,其能量 E 可為:
有時使用角頻率 ω=2πν :
許多物理量可以量子化。譬如角動量量子化。 J 為一個具有鏇轉不變數的系統全部的角動量, Jz 為沿某特定方向上所測得的角動量。其值:
因此, 可稱為 "角動量量子"。
普朗克常數也使用於海森堡不確定原理。在位移測量上的不確定量(標準差) Δx ,和同方向在動量測量上的不確定量 Δp,有如下關係:
還有其他組物理測量量依循這樣的關係,例如能量和時間。

