定義
一個平面圖形 L繞平面上某點 O旋轉 α(0< α<360)後得到的新圖形 L*如果與 L完全重合，則稱 L是 平面旋轉對稱圖形，並稱 L具有 旋轉對稱性。稱點 O為平面旋轉圖形 L的 旋轉中心，稱 α為平面旋轉圖形 L的 旋轉角。
性質
1.如果 α是平面旋轉圖形 L的 旋轉角，那么 α的正整數倍 n α(0< nα<360也一定是平面旋轉圖形 L的 旋轉角。
通常被稱為平面旋轉圖形 L的旋轉角 α是指 最小旋轉角，即對於任何一個在0到 α之間的角度 β都不是這個平面旋轉圖形 L的旋轉角。
圓是旋轉對稱圖形中唯一沒有確定正實數值 α(0< α<360)為其旋轉角的旋轉對稱圖形。
2.如果平面旋轉圖形 L的不是圓， α是平面旋轉圖形 L的旋轉角，那么 α/360必是小於1的正有理數 R。
如果這裡的可以表示為既約分數 m/ n，則 β= α/ m=2 π/ n是平面旋轉圖形 L的指最小旋轉角。
判定
旋轉對稱圖形（1）若函式f（θ）（θ∈ R）滿足f（θ+α）=f（θ）（0<α<360），則極坐標系中曲線L：ρ=f（θ）是旋轉對稱圖形， α是平面旋轉圖形 L的旋轉角。
（2）若函式f（θ）（θ∈ R）滿足f（θ+α）=﹣f（θ）（0<α<π），則極坐標系中曲線L：ρ=f（θ）是旋轉對稱圖形，2 α是平面旋轉圖形 L的旋轉角。
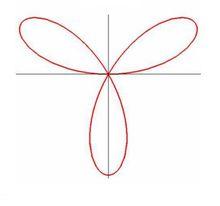
例如：當f（θ）=sin3θ（θ∈ R）滿足f（θ+π/3）=﹣f（θ）。極坐標系中曲線L：ρ=sin3θ是以2π/3為旋轉角的旋轉對稱圖形（三葉玫瑰線）。
旋轉對稱圖形定義（2）中的旋轉角2 α未必是平面旋轉圖形 L的最小旋轉角，例如：當f（θ）=sin2θ（θ∈ R）滿足f（θ+π/2）=﹣f（θ）。極坐標系中曲線L：ρ=sin2θ是以π為旋轉角的旋轉對稱圖形，但是實際上π/2才是平面旋轉圖形 L（四葉玫瑰線）的最小旋轉角。
以上判定條件均是充分條件。
性質
中華台北奧林匹克委員會會標（1）所有的中心對稱圖形都是旋轉對稱圖形。例如：線段、正2n邊形、平行四邊形、圓都是旋轉對稱圖形。
常見的旋轉對稱圖形有：線段、正多邊形、平行四邊形、圓 等。
（2）有兩條（或更多）相交對稱軸的軸對稱圖形都是旋轉對稱圖形。例： 正n邊形（最小旋轉角為360/ n）、圓、五角星（最小旋轉角為360/5即72）、中華台北奧林匹克委員會梅花圖案徽標的輪廓等。
特殊例子
中華人民共和國香港特別行政區區徽香港特別行政區區徽紫荊花圖案是一個以72°為旋轉角的旋轉對稱圖形，但她既不是軸對稱圖形，也不是中心對稱圖形。
