基本內容
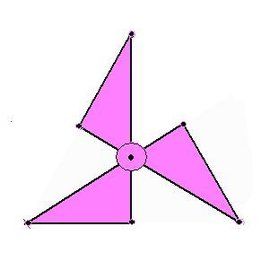 72°鏇轉對稱圖形
72°鏇轉對稱圖形把一個圖形繞著一個定點鏇轉一個角度α後,與初始的圖形結合,這種圖形就叫做鏇轉對稱圖形,這個定點就叫做鏇轉對稱中心,鏇轉的角度叫做鏇轉角。(鏇轉角α滿足0°<α≦180°,且α可以整除360°)>
註:中心對稱也是鏇轉對稱的一種的特別形式。

把一個圖形繞著一條直線(稱為對稱軸或鏇轉軸)鏇轉一個角度360°/n(n為大於1的正整數)後,與初始的圖形重合,這種圖形就叫做鏇轉對稱圖形,這個定點就叫做鏇轉對稱中心,鏇轉的角度叫做鏇轉角。
 72°鏇轉對稱圖形
72°鏇轉對稱圖形把一個圖形繞著一個定點鏇轉一個角度α後,與初始的圖形結合,這種圖形就叫做鏇轉對稱圖形,這個定點就叫做鏇轉對稱中心,鏇轉的角度叫做鏇轉角。(鏇轉角α滿足0°<α≦180°,且α可以整除360°)>
註:中心對稱也是鏇轉對稱的一種的特別形式。
鏇轉對稱圖形:把一個平面圖形繞著平面上一個定點鏇轉(弧度)後,與初始圖形重合,這種圖形叫做鏇轉對稱圖形,這個定點叫做鏇轉對稱中心,鏇轉的角度叫做鏇轉角。...
定義 性質 判定 性質 特殊例子對稱群(symmetric group),設X是一個集合(可以是無限集),X上的一個雙射:a:X→X(即是置換)。集合X上的所有置換構成的族記為S(x)...
定義 對稱群 類型對稱,就是物體相同部分有規律的重複。晶體具有對稱性,這表現在晶體外形上是相等的晶面、晶棱和角頂有規律的重複出現。晶體具有對稱性的原因不同於其他物體。
基本解釋 引證解釋 定義 對稱平衡論 案例對稱英文:symmetry ,指圖形或物體兩對的兩邊的各部分,在大小、形狀和排列上具有一一對應的關係對稱,指物體或圖形在某種變換條件(例如繞直線的鏇轉、...
詞語簡介 其它相關 圖書一 圖書二 對稱群對稱函式理論是代數組合學中的一個重要研究領域,它主要研究對稱群和對稱多項式的代數性質和組合性質,在數學的其他分支和數學物理中有廣闊的套用。
對稱 對稱關係 對稱函式 代數中 幾何中對稱字指把單詞或字母進行藝術處理,同時鏇轉180度中心對稱後形成的極具神秘感的圖案。
介紹 分類 相關書籍 中文字型一個物件(如一維、二維或三維中的圖像或信號)的對稱群是指在複合函式運算下不變的所有等距同構所構成的群。其為所考慮之空間的等距同構群中的一個子群。(若沒有...
一維 二維 三維 一般對稱群對稱圖形有很多分類,例如軸對稱圖形:如果一個圖形沿著一條直線對摺後兩部分完全重合,這樣的圖形叫做軸對稱圖形。如果一個圖形繞某一點鏇轉180度,鏇轉後的圖...
軸對稱圖形 中心對稱圖形 鏇轉對稱圖形