簡介
長方形,數學術語,是有一個角是直角的平行四邊形叫做長方形。也定義為四個角都是直角的平行四邊形,同時,正方形是一種特殊的長方形,也是菱形。
長方形長與寬的定義:
第一種意見:長方形長的那條邊叫長,短的那條邊叫寬。
第二種意見:和水平面同方向的叫做長,反之就叫做寬。長方形的長和寬是相對的,不能絕對的說“長比寬長”,但習慣地講,長的為長,短的為寬。
平行四邊形
平行四邊形,是在同一個二維平面內,由兩組平行線段組成的閉合圖形。 平行四邊形一般用圖形名稱加四個頂點依次命名。註:在用字母表示四邊形時,一定要按順時針或逆時針方向註明各頂點。
在歐幾里德幾何中,平行四邊形是具有兩對平行邊的簡單(非自相交)四邊形。 平行四邊形的相對或相對的側面具有相同的長度,並且平行四邊形的相反的角度是相等的。
相比之下,只有一對平行邊的四邊形是梯形。平行四邊形的三維對應是平行六面體。
性質
(1)兩條對角線相等;
 長方形
長方形(2)兩條對角線互相平分;
(3)兩組對邊分別平行;
(4)兩組對邊分別相等;
(5)四個角都是直角;
(6)有2條對稱軸(正方形有4條);
(7)具有不穩定性(易變形);
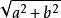 長方形
長方形(8)長方形對角線=;
(9)順次連線矩形各邊中點得到的四邊形是菱形。
判定
矩形的常見 判定 方法:
1. 有一個角是直角的平行四邊形是矩形。( 定義)
2.對角線相等的平行四邊形是矩形。
3. 鄰邊互相垂直的平行四邊形是矩形。
4. 有三個角是直角的四邊形是矩形。
5. 對角線相等且互相平分的四邊形是矩形。
6. (通過 平行四邊形) ①在平行四邊形 ABCD中: ∠ BAD=90°或 BD= AC ∴平行四邊形 ABCD為矩形。
7. (通過 四邊形) ③在四邊形 ABCD中: ∠ ABC=∠ BCD=∠ CDA=90°, ∴四邊形 ABCD為矩形。
面積公式
公式
長方形面積=長×寬
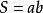 長方形
長方形教學目標
1、使學生在理解面積意義的基礎上,理解計算長方形面積其實就是在求長方形中包含的相應面積單位的個數。
2、使學生經歷長方形面積計算方法的抽象提煉過程,掌握長方形面積計算的一般方法,並能解決一些實際問題。
3、通過探索長方形面積計算一般方法的過程,使學生深人理解平面圖形面積計算的一般思路,提高學生數學學習的能力。
周長公式
公式
長方形周長=(長+寬)×2
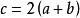 長方形
長方形相關教學
長方形周長的定義是在學生對長方形有了初步認識的基礎上提出來的。教學時,要善於引導學生觀察、歸納、總結,從而培養學生能力。教學中,教師可先出示長方形模型讓學生觀察,並提問:這個長方形有幾條邊?幾個角?對邊有什麼關係?通過直觀演示,學生就會觀察總結出有長方形有4條邊,4個角,對邊相等。然後,教師再用一條細繩沿長方形教具四條邊圍一圈,引導學生觀察,再讓一名學生演示,從而歸納出長方形周長的定義就是繞長方形一周的長度。這樣,通過教師的操作和啟發引導,加深學生了對定義的理解,培養了學生的觀察、歸納、總結能力。
長方形周長計算公式是本節課的教學重點,教師要加以重點講解。不但要讓學生記住公式的內容,而且要知道它是怎樣推導出來的。如:教學長方形周長計算公式時,教師可先出示用鐵絲圍成的模型,引導學生回憶定義,總結出這個長方形周長就是這段鐵絲的長,然後教師把鐵絲展開,啟發學生根據教師的演示導出公式:長方形的周長=長+寬+長+寬。在此基礎上再出示模型,啟發學生通過觀察並結合算式提問,找出規律,從而得出長方形周長公式:(長+寬)X2。這樣,可使學生在推導公式過程中,提高分析能力。

