定義
曲線擬合，俗稱 拉曲線，是一種把現有數據透過數學方法來代入一條數式的表示方式。
在MATLAB的NAG Foundation Toolbox中也有一些曲面擬合函式，如e02daf是最小二乘平方曲面擬合函式，e02def可求出曲面擬合的函式值。
MATLAB軟體提供了基本的曲線擬合函式的命令 ．
擬合直線或多項式曲線
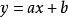數據擬合方程在笛卡爾平面上是一條直線，而這條直線的斜率是 a。因為任何兩點可以決定一條直線，因此總能找到次數不多於1的多項式來串起任何兩個x值相異的點。
如果把多次式的次數增加到2
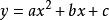數據擬合。
那么只要給定x值各異的3點，總會有次數不多於2的多項式可以把它們串起。
如果把多次式的次數再增加到3
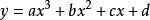數據擬合。
那么只要給定x值各異的4點，總會有次數不多於3的多項式可以把它們串起。
對於這條多項式，更正確的描述是這條多項式附合任何4個 限制。限制可以是一點（x,y）、角度或曲率（即半徑的倒數 1/ R）。角度和曲率的限制通常在曲線的終端，因此稱為 終端條件。為了樣條(spline) 的交接平滑，通常會用到全等的終端條件。 也可以增加如曲率變化等高階約束。例如，在高速公路立體交叉點cloverleaf的設計中，可以用來理解當汽車繞著交叉點運動時作用在汽車上的力，並依此設定合理的限定時速。
一次多項式也可以擬合一個單點和一個角度，三次多項式則可以擬合兩點，一個角度約束以及一個曲率約束。許多其它類型的約束組合也同樣可以用低階或者高階多項式來擬合。
如果有超過n+1個約束（n是多項式的階次），仍然可以使用多項式擬合。通常一個滿足所有約束的精確擬合不一定能夠得到（但是有可能得到，例如，用一次多項式擬合共線的三點三點共線）。通常，我們需要使用一些方法來評價擬合的好壞。最小平方法就是用來評價差別的一種常用的方法 。
Matlab實現方法
多項式函式擬合
a=polyfit(xdata,ydata,n)
其中n表示多項式的最高階數，xdata，ydata為將要擬合的數據，它是用數組的方式輸入．輸出參數a為擬合多項式 的係數 ,相對應的次數為由高到低。
多項式在x處的值y可用下面程式計算。
y=polyval(a,x)
有了x和y就可以把擬合的圖形畫出來，並且同時與原圖對比
plot(xdata,ydata,x,y)
一般的曲線擬合
p=curvefit(‘Fun’,p0,xdata,ydata)
其中Fun表示函式Fun(p,data)的M函式檔案，p0表示函式的初值．curvefit()命令的求解問題形式是
若要求解點x處的函式值可用程式f=Fun(p,x)計算。
例如已知函式形式 ，並且已知數據點 要確定四個未知參數a，b，c，d．
使用curvefit命令，數據輸入 ；初值輸 ；並且建立函式 的M檔案（Fun．m）．若定義 ，則輸出
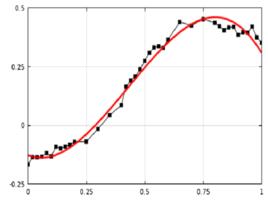
曲線擬合實驗圖
利用COMSOL Multiphysics 擬合實驗，見下圖1 。
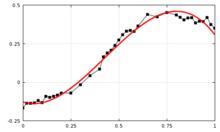圖1 曲線擬合樣圖