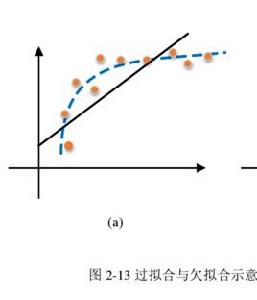
簡介
機器學習的基本問題是利用模型對數據進行擬合,學習的目的並非是對有限訓練集進行正確預測,而是對未曾在訓練集合出現的樣本能夠正確預測。模型對訓練集數據的誤差稱為經驗誤差,對測試集數據的誤差稱為泛化誤差。模型對訓練集以外樣本的預測能力就稱為模型的泛化能力,追求這種泛化能力始終是機器學習的目標。過擬合和欠擬合是導致模型泛化能力不高的兩種常見原因,都是模型學習能力與數據複雜度之間失配的結果。“欠擬合”常常在模型學習能力較弱,而數據複雜度較高的情況出現,此時模型由於學習能力不足,無法學習到數據集中的“一般規律”,因而導致泛化能力弱。與之相反,“過擬合”常常在模型學習能力過強的情況中出現,此時的模型學習能力太強,以至於將訓練集單個樣本自身的特點都能捕捉到,並將其認為是“一般規律”,同樣這種情況也會導致模型泛化能力下降。過擬合與欠擬合的區別在於,欠擬合在訓練集和測試集上的性能都較差,而過擬合往往能較好地學習訓練集數據的性質,而在測試集上的性能較差。在神經網路訓練的過程中,欠擬合主要表現為輸出結果的高偏差,而過擬合主要表現為輸出結果的高方差 。
解決方法
過擬合和欠擬合是所有機器學習算法都要考慮的問題,其中欠擬合的情況比較容易克服, 常見解決方法有:
•增加新特徵,可以考慮加入進特徵組合、高次特徵,來增大假設空間;
•添加多項式特徵,這個在機器學習算法裡面用的很普遍,例如將線性模型通過添加二次項或者三次項使模型泛化能力更強;
•減少正則化參數,正則化的目的是用來防止過擬合的,但是模型出現了欠擬合,則需要減少正則化參數;
•使用非線性模型,比如核SVM 、決策樹、深度學習等模型;
•調整模型的容量(capacity),通俗地,模型的容量是指其擬合各種函式的能力。
•容量低的模型可能很難擬合訓練集;使用集成學習方法,如Bagging ,將多個弱學習器Bagging。
偏差與方差
偏差又稱為表觀誤差,是指個別測定值與測定的平均值之差,它可以用來衡量測定結果的精密度高低。在統計學中,偏差可以用於兩個不同的概念,即有偏採樣與有偏估計。一個有偏採樣是對總樣本集非平等採樣,而一個有偏估計則是指高估或低估要估計的量。方差在機率論和統計方差衡量隨機變數或一組數據時離散程度的度量。機率論中方差用來度量隨機變數和其數學期望(即均值)之間的偏離程度。統計中的方差(樣本方差)是每個樣本值與全體樣本值的平均數之差的平方值的平均數。
在機器學習中,偏差描述的是根據樣本擬合出的模型輸出結果與真實結果的差距,損失函式就是依據模型偏差的大小進行反向傳播的。降低偏差,就需要複雜化模型,增加模型參數,但容易造成過擬合。方差描述的是樣本上訓練出的模型在測試集上的表現,降低方差,繼續要簡化模型,減少模型的參數,但容易造成欠擬合。根本原因是,我們總是希望用有限的訓練樣本去估計無限的真實數據。假定我們可以獲得所有可能的數據集合,並在這個數據集上將損失函式最小化,則這樣的模型稱之為“真實模型”。但實際套用中,並不能獲得且訓練所有可能的數據,所以真實模型一定存在,但無法獲得 。
泛化能力
泛化能力(generalization ability)是指機器學習算法對新鮮樣本的適應能力。學習的目的是學到隱含在數據對背後的規律,對具有同一規律的學習集以外的數據,經過訓練的網路也能給出合適的輸出,該能力稱為泛化能力。通常期望經訓練樣本訓練的網路具有較強的泛化能力,也就是對新輸入給出合理回響的能力。應當指出並非訓練的次數越多越能得到正確的輸入輸出映射關係。網路的性能主要用它的泛化能力來衡量。