簡介
在科學技術的各領域中，不同變數之間的相互關係通常用函式描述。有些函式關係可由經典理論分析推導得出，不僅為進一步的分析研究工作提供理論基礎，也可以方便的解決實際工程問題。但是，很多工程問題難以直接推導出變數之間的函式表達式，或者即使能得出表達式，公式也十分複雜，不利於進一步的分析與計算。由於研究需要，希望能得到這些變數之間的函式關係，這時就可以利用曲線擬合方法，用已知的實驗數據結合數學方法得到變數之間的近似函式表達式。而在處理實驗數據時，常用的是最小二乘法。
在實際的數據擬合問題研究中一般分為線性數據擬合和非線性數據擬合。其中，線性數據擬合通常是採用一組簡單的、線性無關的基函式來逼近試驗數據。而對於非線性數據擬合問題，通常分為兩種情形進行處理，一種是利用變數代換，將其轉為線性問題再求解。另一種是不能線性化的問題，處理起來比較麻煩，可以用MATLAB等程式來實現。
定義
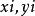非線性數據擬合
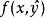非線性數據擬合
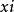非線性數據擬合設有實驗數據（ ），（i=1,2,3....n)，尋找函式 ，使得函式在點 處的觀測值與觀測數據偏差的平方和達到最小。解決此類問題，有以下幾個步驟：首先做出散點圖，確定函式類別；根據已知數據確定待定函式的初始值，用MATLAB軟體計算最佳參數；根據可決係數u，比較擬合結果。
方法
為了實現非線性數據擬合，首先要定義函式，通常採用inline定義的函式用於曲線擬合、數值計算。
步驟：1、建立M檔案；
2、fun=inline('f(x)','參變數','x').
在實際問題中，有時散點圖做出後未必是多項式的圖形，可能像其他的曲線，這是可以猜測曲線類型，然後利用如下命令：
[beta,r,J]=nlinfit(x，y，fun，beta0)
其中，x y為原始數據，fun是在M檔案中定義的函式，beta0是函式中參數的初始值；beta為函式的最優值，r是各點處的擬合殘差，J為雅克比矩陣的數值。
MATLAB實現
LSQNONLIN 解決非線性最小二乘法問題，包括非線性數據擬合問題；LSQCURVEFIT 解決非線性數據擬合問題，下面給出利用這兩個函式的例子。
LSQNONLIN
下面的例子說明利用LSQNONLIN函式用下面的函式進行擬合：
f = A + B exp(C*x)+D*exp(E*x)
對數據集x與y進行擬合，其中y是在給定x的情況下的期望輸出(可以是方程給出數組，也可以是單獨數據組成的數組)。
為了解決這個問題，先建立下面的名為 fit_simp.m的函式，它利用數據x與y，將他們作為最佳化輸入參數傳遞給LSQNONLIN。利用給定的數據x計算f的值，再與原始數據y進行比較。經驗值與實際計算出的值之間的差異作為輸出值返回。LSQNOLIN函式就是最小化這些差的平方和。
function diff = fit_simp(x,X,Y)
A = x(1);B = x(2);C = x(3);D = x(4);E = x(5);
diff = A + B.*exp(C.*X)+D.*exp(E.*X)-Y;
下面的腳本是利用上面定義的fit_simp.m函式的一個例子：
>> X=0:.01:.5;
>> Y=2.0.*exp(5.0.*X)+3.0.*exp(2.5.*X)+1.5.*rand(size(X));
>> X0=[1 1 1 1 1]';
>> options=optimset('Largescale','off');
>> x=lsqnonlin(@fit_simp,X0,[],[],options,X,Y);
Optimization terminated successfully:
Gradient in the search direction less than tolFun
Gradient less than 10*(tolFun+tolX)
>> Y_new=x(1)+x(2).*exp(x(3).*X)+x(4).*exp(x(5).*X);
>> plot(X,Y,'+r',X,Y_new,'b');
注意：LSQNONLIN 只可以處理實數變數。在處理包括複數變數的實例的擬合的時候，數據集應該被切分成實數與虛數部分。
下面給出一個例子演示如何對複數參數進行最小二乘擬合。
為了擬合複數變數，你需要將複數分解為實數部分與虛數部分，然後把他們傳遞到函式中去，這個函式被LEASTSQ作為單個輸入調用。首先，將複數分解為實部與虛部兩個向量。其次，將這兩個向量理解成諸如第一部分是實部、第二部分是虛部。在MATLAB函式中，重新裝配複數數據，並用你想擬合的複數方程計算。將輸出向量分解實部與虛部，將這兩部分連線為一個單一的輸出向量傳遞迴LEASTSQ。
下面，給出一個例子演示如何根據兩個複數指數擬合實數X與Y。
建立方程：
function zero = fit2(x,X,Y)
cmpx = x(1:4)+i.*x(5:8);
zerocomp = cmpx(1).*exp(cmpx(2).*X) +
cmpx(3).* exp(cmpx(4).*X)-Y;
numx = length(X);
zero=real(zerocomp);
zero(numx+1:2*numx)=imag(zerocomp);
Y = a*exp(b*X)+c*exp(d*X);
>> X=0:.1:5;
>> Y=sin(X);
>> Y=Y+.1*rand(size(Y))-.05;
>> cmpx0=[1 i 2 2*i];
>> x0(1:4)=real(cmpx0);
>> x0(5:8)=imag(cmpx0);
>> x=leastsq(@fit2,x0,[],[],X,Y);
>> cmpx=x(1:4)+i.*x(5:8);
>> Y1=real(cmpx(1).*exp(cmpx(2).*X)+cmpx(3).*exp(cmpx(4).*X));
>> plot(X,Y1,'r');
>> hold on
>> plot(X,Y,'+');
LSQCURVEFIT
利用此函式可以在最小二乘意義上解決非線性曲線擬合（數據擬合）問題。也就是說，給定輸入數據xdata，以及觀測的輸出數據ydata，找到係數x，使得函式F(x，xdata)能夠最好的擬合向量值。LSQCURVEFIT利用與LSQNONLIN相同的算法。它的目的在於專門為數據擬合問題提供一個接口。在擬合的時候，2維、3維或者N維參數擬合是沒有什麼差別的。
下面給出一個3維參數擬合的例子。待擬合函式是：
z = a1*y.*x..^2+a2*sin(x)+a3*y.^3;
function F = myfun(a, data);
x = data(1,:);
y = data(2,:);
F= a(1)*y.*x.^2+a(2)*sin(x)+a(3)*y.^3;
下面的腳本展示了這么利用上面的函式：
>> xdata= [3.6 7.7 9.3 4.1 8.6 2.8 1.3 7.9 10.0 5.4];
>> ydata= [16.5 150.6 263.1 24.7 208.5 9.9 2.7 163.9 325.0 54.3];
>> zdata= [95.09 23.11 60.63 48.59 89.12 76.97 45.68 1.84 82.17 44.47];
>> data=[xdata; ydata];
>> a0= [10, 10, 10];
>> [a, resnorm] = lsqcurvefit(@myfun,a0,data,zdata)
Maximum number of function evaluations exceeded;
increase options.MaxFunEvals
a = 0.0088 -34.2886 -0.0000
resnorm = 2.2636e+004
>> format long
>> a
a = 0.00881645527493 -34.28862491919983 -0.00000655131499
>> option=optimset('MaxFunEvals',800);
>> option=optimset('MaxFunEvals',800);
>> [a, resnorm] = lsqcurvefit(@myfun,a0, data, zdata, [], [], option)
Optimization terminated successfully:
Relative function value changing by less than OPTIONS.TolFun
a = 0.00740965259653 -20.21201417111138 -0.00000502014964
resnorm = 2.195886958305428e+004
