定義
設P是由一些複數組成的集合,其中包括0與1,如果P中任意兩個數的和、差、積、商(除數不為0)仍是P中的數,則稱P為一個數域。
常見數域: 複數域C;實數域R;有理數域Q。
(注意:自然數集N及整數集Z都不是數域。)
說明:
1)若數集P中任意兩個數作某一運算的結果仍在P中,則說數集P對這個運算是封閉的。
2)數域的等價定義:如果一個包含0,1在內的數集P對於加法,減法,乘法與除法(除數不為0)是封閉的,則稱數集P為一個數域。
數域的性質定理
(1)任意數域P都包括有理數域Q;即,有理數域為最小數域。
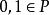 數域
數域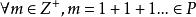 數域
數域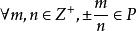 數域
數域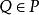 數域
數域證明:設P為任意一個數域,由定義可知,,於是有,進而有,而任意一個有理數可表成兩個整數的商,所以。
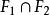 數域
數域(2)設F1及F2是兩個數域,則也構成一個數域。
舉例
數域因為其定義過於廣泛,沒有太好的性質,在數學中的直接套用很少,經常用到的是它的一些子對象,例如:
 數域
數域 數域
數域 數域
數域代數數域,即有理數域的有限擴張,例如有理數域和高斯域。
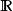 數域
數域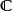 數域
數域阿基米德局部域,實數域和複數域,它們是代數數域關於通常的絕對值做完備化得到的域。
 數域
數域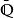 數域
數域的代數閉包。
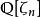 數域
數域 數域
數域 數域
數域 數域
數域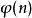 數域
數域分圓域,它是有理數域的射線類域(ray class field),即所有的有限阿貝爾擴張均包含在某個分圓域中。它也是代數數域,擴張次數是的歐拉函式。

