庫默爾擴張

一種阿貝爾擴張，因首先由E.E.庫默爾研究而得名。阿貝爾擴張是代數數論研究的主要對象。

正文

　庫默爾擴張和分圓域則是阿貝爾擴張的兩個重要類型。一個阿貝爾擴張K/k稱為庫默爾擴張,指的是存在一個正整數m使得:①域k的特徵ch(k)不能整除m，而且 k包含m次本原單位根ζ；②K/k的伽羅瓦群 Gal(K/k)的每個元素的階整除m 。此時K/k又特別稱為指數是m的庫默爾擴張。以下考慮的都是在一個給定的滿足條件①的基域k上的一切指數為m的庫默爾擴張。用k*表示k中非零元素乘法群,用km表示k*中元素的m次冪構成的子群。
庫默爾擴張的子擴張是庫默爾擴張。任意多個庫默爾擴張的複合域還是庫默爾擴張。
在域k滿足條件①的前提下，則在k上添加k*的一個元素α 的m 次根而得到根擴張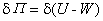是一個指數為m的庫默爾擴張，而且Gal(K/k)是一個循環群。反之，任一指數為m 的循環庫默爾擴張K/k是一個根擴張K=k(θ)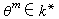，,而且θ可由拉格朗日的預解式求得。設【K:k】=n,Gal(K/k)=〈σ〉,α為K的任一個本原元素。ξ為k中任一個n次本原單位根，於是預解式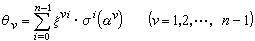

中任一個非零的θυ都可取作θ。但θ的取法不是惟一的。
任一庫默爾擴張K/k是一些循環庫默爾擴張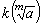的複合域,其中α取遍k*的一個子集S 的元素。K確定K*的一個子群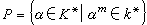,則K=k(P),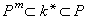。子群P由這些條件惟一確定。令h=Pm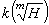，表示所有根擴張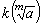（其中 α∈h）的複合域，則有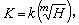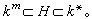子群h由上述條件惟一決定。反之,給定k*的一個子群h′使得km嶅h′，則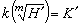是k上的一個庫默爾擴張。令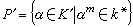,則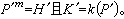這樣,k上庫默爾擴張K 和k*的包含km的子群h成一一對應,而且對應關係由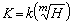確定。
設K/k為任一庫默爾擴張,G=Gal(K/k)而且設P和h定義如上。對於σ∈G,λ∈P,有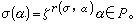定義映射G×P→<ζ>如下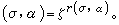：它滿足①(στ,λ)=(σ,λ)(τ,λ)，②(σ,λβ)=(σ,λ)(σ,β)，③(σ,P)=1匔σ=1,④(G,λ)=1匔λ∈k*,每個σ∈G確定P 的一個特徵ⅹσ 使得ⅹσ(λ)＝(σ，λ)。而且Ker(ⅹσ)払k*，因而ⅹσ誘導出商群P/k*的一個特徵。反之,P/k*的每個特徵ⅹ可以提升為P的一個特徵ⅹ′使得Ker(ⅹ′)払k*，而且ⅹ′決定P的一個自同構 λ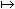ⅹ′(λ)·λ,並且保持 k*的元素不動,這個自同構可以開拓成庫默爾擴張K的一個k自同構。所以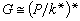，其中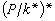表示 P/k*的特徵群。另一方面,P 到h 的冪映射α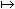αm誘導出同構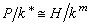，最後得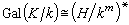。這個同構可以由雙線性映射G×h→<ζ>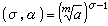：來實現,即每個σ∈G 映到h 的特徵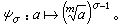
特別，若K/k是有限庫默爾擴張，則有

E.阿廷和O.施賴埃爾推廣了庫默爾擴張的理論。設k為一個特徵p>0的域，若K/k是阿貝爾擴張,其伽羅瓦群的指數是p，則稱K/k是指數為p的阿貝爾擴張，或阿廷-施賴埃爾擴張。令 β(X)表示Xp-X,β-1(α)表示多項式β(X)-α 的任一根。令β(k)={β(α)｜α∈k},則β(k)是加法群k的一個子群。多項式β(X)-α在k上不可約的充分必要條件是α∈k，但α唘β(k)。
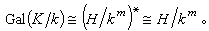
設K/k為一個p次阿貝爾擴張,Gal(K/k)=〈σ〉。則存在一個元素α∈K使得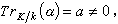令

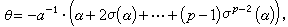
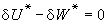則K=k(θ)，θ為的一根。反之，設α∈k但α唘β(k)，則β(X)- α在k上的分裂域是k上一個p次阿貝爾擴張。
設K/k 是任一指數為p 的阿廷-施賴埃爾擴張，G=Gal(K/k)。則K是一?I>p次阿廷-施賴埃爾擴張k(β-1(α))的複合域，α∈S嶅k，S為 k的一個子集。令T={α∈K｜β(α)∈k},則T為K的一個加法子群,而且K=k(T),β(T)嶅k嶅T。令N =β(T)，則N 為k 的一個加法子群。令k(β-1(N))表示 k(β-1(α))（其中α∈N）的複合域，則有K=k(β-1(N))，β(k)嶅N嶅k。反之,設N′為k的一個加法子群,且β(k)嶅N,則K′=k(β-1(N′))是一個指數p的阿廷-施賴埃爾擴張。總之,k上指數p 的阿廷-施賴埃爾擴張和k中包含β(k)的加法子群N 成一一對應，而且對應關係由下式確定：K=k(β-1(N))。
設K/k 為任一指數 p 的阿廷－施賴埃爾擴張，G=Gal(K/k)，T、N定義如上,並設Fp為特徵p的素域,定義G×T 到Fp的映射(σ,α)=σ(α)-α。這是一個雙線性映射，而且(σ,T)=0匔σ=1，(G,α)=0匔α∈k。每個σ∈G確定T的一個特徵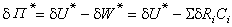又誘導出商群T/k的一個特徵。
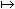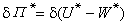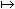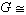
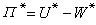
反之，T/k的每個特徵ⅹ可提升為T的一個特徵ⅹ┡。ⅹ┡決定T 的一個自同構αα+ⅹ┡(α)。這個自同構可以開拓成K的一個k自同構。所以。T 到N 的同態映射 αβ(α)誘導出同構 T/k≌ N/β(k)。於是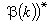。 這個同構可由雙線性映射G ×N→Fp： (σ,α)=(σ-1)β-1(α)來實現,即每個σ∈G決定N/β(k)的一個特徵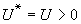
E.維特引進了一個特徵p>0的域k上的向量運算，從而得到維特向量環。E.維特利用這個向量環將E.阿廷和O.施賴埃爾關於指數p的阿廷-施賴埃爾擴張理論推廣到任意指數pe(e≥1)的阿廷-施賴埃爾擴張上去。
關於數域上的庫默爾擴張的算術理論，在這裡僅介紹一個最簡單的情況。設k為一個數域,而且包含一個素數l次本原單位根ζ,又設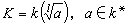，但 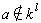，P是k的一個素理想。P在K中的分解只有三種情況：P在K中仍然保持為素理想,稱之為惰性的；或者P在K中等於一個素理想的l次冪,稱之為分歧的；或者P在K中分解成l個不同素理想的積,稱之為分裂的。設主理想(α)含P的方冪為Pe。於是有下列結果：
若l凲e，則P在K中分歧；若l｜e但P凲( l),則P在K內不分歧,此時可將α化為e=0的情況，於是，若還有同餘式Xc(n)呏α(modP)在k內有解，則P在K中分裂，否則P在K中為惰性的;設l｜e,且P｜(l)。此時首先將α化為e=0的情況。設主理想(1-ζ)含素因子P的方冪為Pr,則有：①若同餘式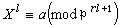在k中有解，則P在K內分裂。②若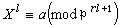在k中無解，但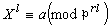在k中有解，則P在K內是惰性的。③若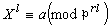在k中無解，則P在K內分歧。

配圖

相關連線