P進數域

P進數域是一類特殊的局部域。設局部域K的特徵數為，當K為∞時，K是伽羅瓦域GF(p)上的p進數域(c=1)，或是p進數的有限次代數擴張；這裡p為素數。

簡介

P進數域是一類特殊的局部域。

設局部域K的特徵數為：

當為有限數時，K是伽羅瓦域GF(p )上的p級數域(c=1)，或是p級數域的有限次代數擴張(c>1)；

當K為∞時，K是伽羅瓦域GF(p )上的p進數域(c=1)，或是p進數的有限次代數擴張；這裡p為素數。

模

p級數域

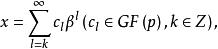P進數域

p級數域是GF(p )上的形式冪級數域，亦即其元x可寫為x+y與xy都是按位進行模p運算的（不進位）。

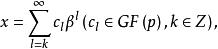p進數域

P進數域

p進數域中的模p的元x也是表示，只是x+y與xy是按位進行模p運算且自左向右進位。公式中的p∈K是K的生成元。

局部域

在數學上，局部域是一類特別的域，它有非平凡的絕對值，此絕對值賦予的拓撲是局部緊的。

局部域可粗分為兩類：一種的絕對值滿足阿基米德性質（稱作阿基米德局部域），另一種的絕對值不滿足阿基米德性質（稱作非阿基米德局部域）。在數論中，數域的完備化給出局部域的典型例子。