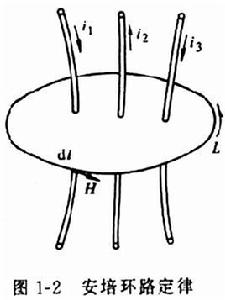
簡介
它的數學表達式是
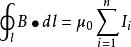 安培環路定理
安培環路定理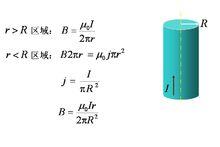 安培環路定理套用
安培環路定理套用按照安培環路定理 ,環路所包圍電流之正負應服從右手螺鏇法則。如果閉合路徑l包圍著兩個流向相反的電流I和I( 如左圖所示)
按圖中選定的閉合路徑l 的繞行方向,B矢量沿此閉合路徑的環流為
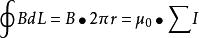 安培環路定理
安培環路定理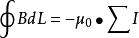 安培環路定理
安培環路定理如果閉合路徑l包圍的電流等值反向,或者環路中並沒有包圍電流,則:
積分形式
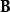 安培環路定理
安培環路定理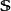 安培環路定理
安培環路定理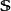 安培環路定理
安培環路定理 安培環路定理
安培環路定理電流I在一個曲面 上的通量,等於B場沿著 的邊緣閉合迴路 的路徑積分。採用國際單位制,原版安培定律的積分形式可以寫為:
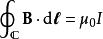 安培環路定理
安培環路定理。
請注意到這方程有些模糊之處,需要特別澄清:
 安培環路定理
安培環路定理 安培環路定理
安培環路定理第一,邊界曲線 的正向與曲面 的側符合右手規則。
 安培環路定理
安培環路定理 安培環路定理
安培環路定理 安培環路定理
安培環路定理第二,(固定 )定理之成立與以 為邊界 的的選擇無關。
安培定律可由畢奧-薩伐爾定律和磁場的疊加性證明(請參閱畢奧-薩伐爾定律)。在靜磁學中,安培定律的角色與高斯定律在靜電學的角色類似。當系統組態具有適當的對稱性時,我們可以利用這對稱性,使用安培定律來便利地計算磁場。例如,當計算一條直線的載流導線或一個無限長螺線管的磁場時,可以採用圓柱坐標系來匹配系統的圓柱對稱性。
微分形式
根據開爾文-斯托克斯定理,這方程也可以寫為微分形式。只有當電場不含時間的時候,也就是說,當電場對於時間的偏微分等於零的時候,這方程才成立。採用國際單位制,這方程表示為
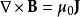 安培環路定理
安培環路定理。
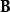 安培環路定理
安培環路定理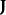 安培環路定理
安培環路定理磁場 的鏇度等於(產生該磁場的)傳導電流密度 。
缺點
原版安培定律只適用於靜磁學。在電動力學裡,當物理量含時間,有些細節必須仔細檢查。思考安培方程,
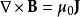 安培環路定理
安培環路定理;
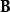 安培環路定理
安培環路定理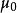 安培環路定理
安培環路定理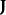 安培環路定理
安培環路定理其中, 是B場, 是磁常數, 是總電流。
取散度於這方程,則會得到
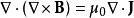 安培環路定理
安培環路定理。
套用一個矢量恆等式,鏇度的散度必定等於零。所以,
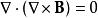 安培環路定理
安培環路定理。
這意味著電流密度的散度等於零:
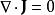 安培環路定理
安培環路定理。
在靜磁學內,這是正確的。但是,出了靜磁學範圍,當電流不穩定的時候,這就不一定正確了。
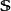 安培環路定理
安培環路定理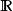 安培環路定理
安培環路定理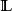 安培環路定理
安培環路定理 安培環路定理
安培環路定理 安培環路定理
安培環路定理一個正在充電的電容器,左邊的圓形金屬板,被一個假想的封閉圓柱表面 包圍。這圓柱表面的右邊表面 處於電容器的兩塊圓形金屬板之間,左邊表面 處於最左邊。沒有任何傳導電流通過表面 ,而有電流 I通過表面 。
 安培環路定理
安培環路定理 安培環路定理
安培環路定理舉個經典例子,如圖右,一個正在充電的電容器,其兩片金屬板會隨著時間分別累積異性電荷。設定表面 的邊緣為閉合迴路 。套用安培定律,
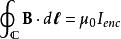 安培環路定理
安培環路定理。
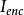 安培環路定理
安培環路定理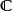 安培環路定理
安培環路定理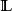 安培環路定理
安培環路定理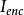 安培環路定理
安培環路定理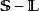 安培環路定理
安培環路定理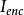 安培環路定理
安培環路定理在這裡, 是通過任意曲面的電流,只要這曲面符合一個條件:邊緣為閉合迴路 。所以,這任意曲面可以是表面 ,而 是I;或者這任意曲面可以是封閉圓柱表面減去左邊表面 ,而由於通過這任意曲面的電流是 0, 是0。選擇不同的曲面會得到不同的答案,這在物理學裡,是絕對不允許發生的事。
為了解決上述難題,安培定律必須加以修改延伸。 套用流體力學的方法,麥克斯韋摹想磁場為電介質渦鏇(vortex)大海,而位移電流即為大海內的電極化電流。在他於1861年發表的論文《論物理力線》裡面,麥克斯韋將位移電流項目加入了安培定律。
證明方法
 安培環路定理
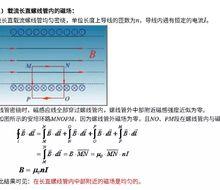
安培環路定理如果在某個載流導體的穩恆磁場中可以找到一條閉合環路l,該環路上的磁感強度B大小處處相等,B的方向和環路的繞行方向也處處同向,載流長直螺線管內磁場 套用安培環路定理 忽略了左右下的部分,證明並不是在環路上B的大小處處相等環路方向與磁感應強度方向相同處,B的大小方向處處相等。
對稱環路
在垂直於長直載流導線的平面內,以載流導線為圓心作一條半徑為r 的圓形環路l,
則在這圓周上任一點的磁感強度H的大小為
其方向與圓周相切.取環路的繞行方向為逆時針方向,取線元矢量dl,則H與dl間的夾角 ,H沿這一環路 l 的環流為
式中積分 是環路的周長。
於是上式可寫成為
從上式看到,H沿此圓形環路的環流 只與閉合環路所包圍的電流I 有關,而與環路的大小、形狀無關。
任意環路
在垂直於長直載流導線的平面內,環繞載流直導線作一條如下圖所示的任意環路l,取環路的繞行方向為逆時針方向。
在環路上任取一段線元dl,載流直導線線上元dl處的磁感強度B大小為
H與dl的夾角為 ,則H對dl的線積分為
直導線中心向線元的張角為 ,則有 ,所以有
可見,H對dl的線積分與到直導線的距離無關。
那么B對整個環路的環流值為
上述計算再次說明H的環流值 與環路的大小、形狀無關。
不包圍電流
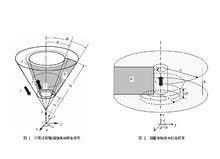 安培環路定理套用
安培環路定理套用在垂直於長直載流導線的平面內,在載流直導線的外側作一條如下圖所示的任意環路l,取環路的繞行方向為逆時針方向。
以載流直導線為圓心向環路作兩條夾角為 的射線,在環路上截取兩個線元 和 。 和 距直導線圓心的距離分別為 和 ,直導線在兩個線元處的磁感強度分別為 和 。從上圖可以看出 ,而 。利用安培環路定理的證明之二的結論可知
結論
所以有:
從載流直導線中心O出發,可以作許多條射線,將環路分割成許多成對的線元,磁感強度對每對線元的標量積之和,都有上式的結果,故 即環路不包圍電流時,B的環流值為零。
安培環路定理反映了磁場的基本規律。和靜電場的環路定理 相比較,穩恆磁場中B 的環流 ,說明穩恆磁場的性質和靜電場不同,靜電場是保守場,穩恆磁場是非保守場。
計算套用
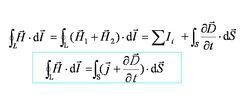 安培環路定理套用
安培環路定理套用利用安培環路定理求磁場的前提條件:如果在某個載流導體的穩恆磁場中,可以找到一條閉合環路l,該環路上的磁感強度B大小處處相等,B的方向和環路的繞行方向也處處同向,這樣利用安培環路定理求磁感強度B的問題,就轉化為求環路長度,以及求環路所包圍的電流代數和的問題,即
利用安培環路定理求磁場的適用範圍:在磁場中能否找到上述的環路,取決於該磁場分布的對稱性,而磁場分布的對稱性又來源於電流分布的對稱性。因此,只有下述幾種電流的磁場,才能夠利用安培環路定理求解。
1.電流的分布具有無限長軸對稱性
2.電流的分布具有無限大面對稱性
3.各種圓環形均勻密繞螺繞環
利用安培環路定理求磁場的基本步驟
1.首先用磁場疊加原理對載流體的磁場作對稱性分析;
2.根據磁場的對稱性和特徵,選擇適當形狀的環路;
3.利用公式求磁感強度。