紅外輻射
簡史 1666年,英國物理學家I.牛頓發現,太陽光經過三稜鏡後分裂成彩色光帶──紅、橙、黃、綠、青、藍、紫。1800年,英國天文學家F.W.赫歇耳在用水銀溫度計研究太陽光譜的熱效應時,發現熱效應最顯著的部位不在彩色光帶內,而在紅光之外。因此,他認為在紅光之外存在一種不可見光。後來的實驗證明,這種不可見光與可見光具有相同的物理性質,遵守相同的規律,所不同的只是一個物理參數──波長。這種不可見光稱為紅外輻射,又稱紅外光、紅外線。17~18世紀,許多物理學家認為,光(包括紅外光和紫外光)具有波動的性質,有一定的傳播速度,波長是它的特徵參數並可以測量。可見光的彩色不同,反映了它們的波長不同。紫光的波長最短,紅光的波長最長,紅外輻射的波長則更長,紫外光的波長比紫光更短。1864年,英國物理學家J.C.麥克斯韋從理論上總結了當時已有的電磁學規律,提出了存在電磁波的可能性,它的傳播速度可用純電學量計算出來。後來的實際測量證明,其傳播速度就是光速。因而猜想,光波就是電磁波。1887年,德國科學家H.R.赫茲用實驗證實了這一猜想。
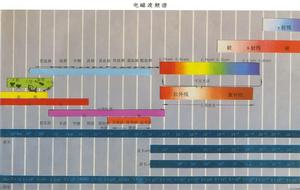
已知帶電體受到擾動就發射出電磁波。擾動越強烈,發射出電磁波的能量就越大,波長就越短。由於受擾動的方式有多種,電磁波的波長範圍很廣。整個電磁波譜各波段的名稱和波長範圍(見彩圖)。
 紅外輻射
紅外輻射λν=c(1)
紅外波段的劃分 電磁波譜劃分為許多不同名稱的波段。主要是根據它們的產生方法、傳播方式、測量技術和套用範圍的不同而自然劃分的。紅外波段又可劃分為近紅外、中紅外、遠紅外三個波段。但劃分的方法則因學科或技術領域不同而異。由於大氣對紅外輻射的吸收,只留下三個“視窗”,即1~3微米、3~5微米、8~13微米,可讓紅外輻射通過。因而在軍事套用上,分別稱這三個波段為近紅外、中紅外、遠紅外波段。8~13微米,也稱為熱波段。
在光譜學中,劃分波段的方法尚不統一。一般分別以0.75~3微米、3~40微米和40~1000微米作為近紅外、中紅外和遠紅外波段。近紅外是可以用玻璃作為透射材料和用硫化鉛探測器進行檢測的波段。中紅外原來是以稜鏡作為色散元件的波段,但後來都採用光柵作為色散元件,40微米這個界限不再有意義。但是,40微米又是石英能讓紅外輻射透過的起始波長,故仍可作為中紅外波段與遠紅外波段的界限。在遠紅外波段的長波端,傳統的幾何光學和微波傳輸技術都不適用,需要發展新的技術。新技術適用的波段也可能是一個新名稱的波段。此外,遠紅外波段內出現雷射,以輻射源是否具有相干性作為遠紅外與微波劃界的標準已不適用。因而暫以1000微米作為遠紅外波段的界限,把波長為1~3毫米的電磁波稱為短毫米波。
輻射的產生 在物質內部,電子、原子、分子都在不斷地運動,有很多可能的運動狀態。這些狀態都是穩定的,各具有一定的能量。通常用“能級”來表示這些狀態。在正常情況下,物質總是處在能量最低的能級上(基態)。如果有外界的刺激或干擾,把適當的能量傳遞給電子、原子或分子,後者就可以改變運動狀態,進入能量較高的能級(激發態)。但是,電子、原子或分子在激發態停留的時間很短,很快就回復到能量較低的能級中去,把多餘的能量釋放出來。釋放能量的方式有多種,最常見的是發射電磁波。根據現代量子論的概念,從較高能級E1回復到較低能級E0時,發射出來的電磁波的頻率為
ν=(E1-E0)/h(2)
式中h為普朗克常數,h=6.626×10-34焦·秒,hν是發射出來的能量單元,稱為光子。因此,輻射是從物質中發射出來的。任何一塊小的物體都包含著極大數目的原子或分子。每個原子或分子都有很多能級,從高能級躍遷到低能級都能發射光子。實際發射出來的電磁波就是這些大量光子的總和。各個原子或分子發射光子的過程基本上是互相獨立的;光子發射的時間有先有後。光子發射時,原子或分子在空間的取向有各種可能,因而光子可向各個方向發射,其電磁場振動也可有各種方向;再加上物體內各能級之間的相互影響,兩能級之間的能量差會有極小的變動。所有這些因素的聯合作用,使所發射出來的輻射包含著各種頻率,沒有一定的相位,沒有一定的偏振,這就是非相干輻射。
現代科學技術能採用適當辦法,迫使某兩個能級之間的光子發射過程都發生在同一時間向同一方向,這就能得到頻帶非常狹窄、方向性極好、強度很高,而且是偏振的相干輻射。這就是雷射。在無線電波和微波範圍內,電磁波的產生是利用電子在真空里的運動,迫使所有電子作相同的運動態的改變,這就發射出單一頻率的、偏振的相干輻射。
輻射雖是從物體內部發射出來的,但必須首先從外界給以擾動,給以能量。這個過程稱為激勵。激勵的方法有多種,其中與紅外輻射關係最為密切的是加熱。因加熱而發射的輻射稱為熱輻射。
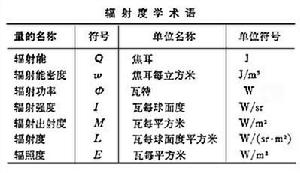
紅外輻射度學 這方面的術語比較複雜,必須區別輻射的發出和接受兩個方面,標明擴展源的方向性。擴展源就是尺寸與測量距離相比不可忽略的輻射源。反之,則可當作點源看待。
表內列出一些主要的輻射度學術語的名稱、符號、單位名稱和單位符號。
 紅外輻射
紅外輻射 紅外輻射
紅外輻射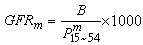 (3)
(3)
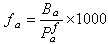 (4)
(4)
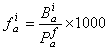 為法線方向單位立體角內的輻射功率。(3)式的定義以單位投影面積dAcosθ計算,因而有
為法線方向單位立體角內的輻射功率。(3)式的定義以單位投影面積dAcosθ計算,因而有 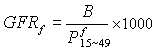
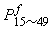 (5)
(5)
輻射出射度 單位面積內向上半球發射的全部輻射功率。
M=dφ/dA (W/m2) (6)
dφ就是(5)式所求的輻射功率,因而M=πL (7)
對於朗伯型表面,這個關係很重要。在實踐中,只要測量法線方向的輻射度就可得到輻射出射度M。對非朗伯型表面,則必須測量射向各個方面的輻射功率,然後積分求M。輻射出射度是指從單位面積發出的輻射功率,可以是物體本身發射的輻射;也可以是被物體反射出來的輻射。此處強調“出”字。如果是指投射到物體表面的輻射,則必須用輻照度來表示。兩者具有相同的量綱。
輻射強度 發射體的整個表面射入某一方向 θ的單位立體角內的輻射功率
I=dφ/dω (W/sr) (8)
把(3)式對面積積分就得到I。在這種情況下,就是把擴展源看成點源。採用強度兩字可與其他點源(電、磁、光)中的相應術語相一致。輻射功率 與輻射能通量的含義相同,但用法略有區別。在討論表面發射的或接受的輻射時宜用輻射功率。在描述空間某一假想平面內的輻射時則宜用輻射能通量。
表中所列各量都是指輻射源發射一定光譜而言的,如果要描述在波長λ 處墹λ間隔內的量,或在頻率ν 處墹ν間隔內的量,則在表中各量的名稱之前加“單色”、“光譜”或“分譜”,符號的右下腳加λ或ν,如θλ,ωλ,φλ,Iλ,Mλ,Lλ,Eλ或θν,φν,Iν,Mν,Lν,Eν等。在僅討論某一單色輻射的情況時,宜用“單色”。在討論整個光譜內的各單色輻射的量時,則宜前面用“分譜”或“光譜”。
由於輻射的各成分是線性疊加的,M=πL關係對單色輻射同樣適用
Mλ=πLλ(9)
熱輻射及其規律 加熱物體物質內部的某些運動狀態升高到激發態,當從激發態回復到較低能量的狀態時,將產生輻射,稱為熱輻射。這種輻射又可能再被物體吸收,激勵某些運動而再引起熱輻射。因而熱輻射過程有可能達到穩定的平衡狀態。例如,考慮有一個密閉的空腔,腔壁用某種材料製成。加熱使它保持在恆定溫度T0。在腔內,腔壁上任一面元dA所發射的輻射總是落在腔壁的另一部分。落在腔壁某部分的輻射,部分被吸收,其餘部分被反射出來又落到腔壁的另一部分。因此,不管從腔壁哪一部分發射出來的輻射,最後總是進入腔壁。在達到熱平衡的條件下,任何面元所產生的輻射,在頻率和強度等方面,總是等於它所吸收的輻射。否則就不是熱平衡。因此,在熱平衡條件下的空腔內部,所有的輻射必定具有穩定不變的性質,僅依賴於腔壁溫度,與腔壁材料的性質無關。黑體輻射 拿一塊任何材料的小物體,放入腔內,不與腔壁接觸。不久,這塊物體就被加熱到與腔壁相同的溫度,即與腔壁達到熱平衡。這時,小物體表面所發出的輻射,在頻率和強度等方面,都必定與它所吸收的輻射相等。設物體表面所接受的輻照度為E(瓦/米2),物體對輻射的吸收比(吸收功率與入射功率之比)為α,它的輻射出射度為M(瓦/米2),則對任一部分表面,熱平衡條件為
M=αE (10)
上式表明,一個物體對輻射的吸收比越大,它的輻射出射度也就越大,即吸收越強的物體發射輻射也越強。這就是基爾霍夫定律。當α=1時,輻射出射度就達到最大。具有這種特性的物體稱為黑體。它所發射的輻射稱為黑體輻射。右上角加肩標“bb”表示黑體輻射的量。
當α=1時,腔內物體所受到的輻照度就是
E=Mbb (11)
換句話說,熱平衡空腔內的輻射就是黑體輻射。因而任意物體的輻射出射度就是M=αMbb (12)
它總是小於黑體的輻射出射度。黑體並不難得,如在上述空腔壁上開一個很小的孔,孔的面積遠遠小於腔壁的面積,則從小孔發射出來的輻射能很小,不足以影響腔內的熱平衡。從外面射入小孔的輻射,經腔壁多次反射,總是全部被吸收掉,不再從小孔反射出來,因而吸收比等於1。帶有小孔的空腔就是黑體,從小孔發射出來的輻射就是黑體輻射。
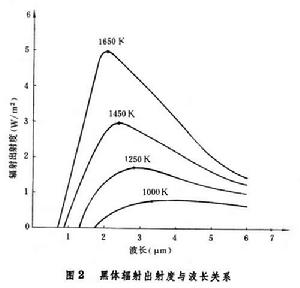
黑體輻射是19世紀末葉研究得最多的物理學問題之一。對空腔發射出來的輻射進行了很多測量,證明黑體輻射屬於朗伯型,它的輻射功率按波長或頻率的分布是穩定的,僅與腔壁溫度有關,與製造腔體的材料無關。圖2為黑體在幾個溫度下,輻射出射度按波長的分布曲線。每個溫度的分布曲線上都出現一個峰值,峰值所在的波長λm 隨溫度升高而向短波移動。
 紅外輻射
紅外輻射斯忒藩定律 黑體的輻射出射度,包括各種波長在內的總輻射功率與黑體溫度(絕對溫標)T 的 4次方成正比
Mbb=σT4 (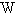 /m2) (13)
/m2) (13)
維恩位移定律 峰值波長λm與黑體溫度T 的乘積為常數
λmT ≈3000
從理論上推導出黑體的輻射出射度對波長(頻率)的分布曲線(圖2),是19世紀末葉極為重要的物理學課題。1900年,M.普朗克提出了一個新的概念,即輻射能並不是連續的,只能以一定的份量被吸收或被發射。這個份量叫做量子(此處也稱光子),它與輻射的頻率成正比。即光子的能量為hν,比例常數h稱為普朗克常數。後來,精確測定證明,h=6.626×10-34焦·秒。 紅外輻射
紅外輻射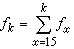 (14)
(14)
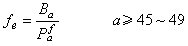 (15)
(15) 式中c為光速;κ為玻耳茲曼常數。這個公式稱為普朗克輻射定律。
這個公式能精確地解釋已有的一切實驗數據,而且還把上述兩經驗公式中的常數用更基本的物理常數表達出來。
普朗克公式不僅可以解釋當時已有的全部實驗事實,而且在60年代以後,天文學家發現宇宙間充滿著一類長波紅外輻射,其波長分布完全與普朗克公式相符,證明宇宙間存在著2.7K背景溫度。
用普朗克公式能精確地計算出黑體輻射,因而黑體已成為輻射測量的標準。已製造出各種形式的黑體,其中有些黑體非常接近理想黑體。按普朗克公式計算出來的黑體輻射數據表已成為紅外工程設計人員的手冊。
更重要的是,普朗克的量子假設開創了20世紀的量子物理學。
一般物體的熱輻射 一般物體對輻射的吸收比總是小於1,因而發射熱輻射的能力也小於黑體。對於它的輻射度,一般不直接測量,而是與同溫度的黑體輻射進行比較,用一個比值表示其輻射特性。
首先,比較熱輻射物體與同溫度黑體在各個方向上的輻射度。前者的輻射度L可寫成
L=ε(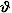 ,ψ)Lbb (16)
,ψ)Lbb (16)
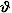 ,ψ)無關。因而達類物體也具有朗伯型表面,M=πL關係同樣適用。
,ψ)無關。因而達類物體也具有朗伯型表面,M=πL關係同樣適用。 其次,比較熱輻射物體與黑體在各個溫度及各波長的法向輻射度。利用上述關係就可得到物體的輻射出射度M
M=ε(T,λ)Mbb(T,λ) (17)
式中ε與波長和熱輻射體的溫度有關。但是,對於一些具有實用價值的熱輻射物體,ε隨λ的變化比較緩慢。在所需要的光譜範圍內,可以把ε看作常數,或者取適當的平均值。這樣,按普朗克公式對波長積分所得的斯忒藩定律可寫成M=ε(T)σT4 (18)
因而,對任一熱輻射物體,都可以用一個比數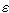 來描述它的熱輻射性能。一般說來,ε是方向、溫度和波長的複雜函式。但是,一些常用的熱輻射體,大都具有朗伯型表面,ε隨λ的變化緩慢,用一個對波長作適當平均的ε(T)就足以描述它的全部熱輻射特性。
來描述它的熱輻射性能。一般說來,ε是方向、溫度和波長的複雜函式。但是,一些常用的熱輻射體,大都具有朗伯型表面,ε隨λ的變化緩慢,用一個對波長作適當平均的ε(T)就足以描述它的全部熱輻射特性。 在前面討論空腔熱平衡時,曾得到式(12),將其與式(18)相比,即得
ε=α (19)
即任何物體的吸收比與發射率在任何溫度和任何波長時都相等。黑體是其中的一個特例,ε=α=1。當α<1時,投射到物體表面的輻射,一部分被反射,其餘部分進入體內被吸收。但是,也有可能僅有一部分被吸收,而其餘部分透過物體輻射出去。如果反射比(反射出去的輻射功率與入射輻射功率之比)為 ρ,透射比(透過物體的輻射功率與入射輻射功率之比)為 τ,則按能量守恆定律,應有
α+ρ+τ=1(20)
對於不透明物體τ=0,則得α+ρ=1
因而有ε=1-ρ(21)
在實踐中,常用測量ρ的辦法來求ε。
幾種常見物體的發射率見表。
 紅外輻射
紅外輻射
