基本介紹
弗雷德霍姆二擇一定理是研究線性橢圓型方程的解存在問題的一個泛函分析定理。下面分別介紹它在賦范空間中的表述和在希爾伯特空間中的表述。
表述1
 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理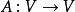 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理在賦范空間中的這個定理表述為:設是賦范線性空間,是一緊線性運算元,則以下兩種可能有一個且只有一個發生:
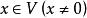 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理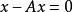 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理1.存在,使得;
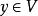 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理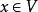 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理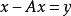 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理2.對於任意,存在惟一的,使得。
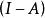 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理在第二種情形下,是有界線性運算元。
表述2
 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理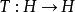 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理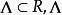 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理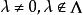 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理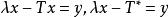 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理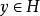 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理希爾伯特空間中的弗雷德霍姆二擇一定理表述如下:設是一個希爾伯特空間,是一個緊線性運算元,則存在一可數集不含非零極限點,使得若,則方程,對每一有惟一解,且逆運算元
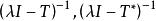 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理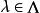 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理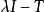 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理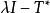 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理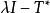 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理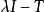 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理有界。若,則運算元和的零空間有正有限維數;若且唯若正交於的零空間,上述第一個方程有解;而若且唯若正交於的零空間,第二個方程有解。
套用
把弗雷德霍姆二擇一定理用於散度形式的橢圓型方程的狄利克雷問題
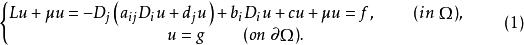 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理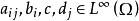 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理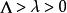 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理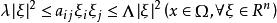 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理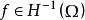 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理則有如下結果:若,且存在常數,使得;又設Ω為使索伯列夫嵌入定理成立的有界區域,,則問題(1)只有以下兩種可能:
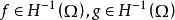 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理1. 對於任意,問題(1)有惟一的弱解。
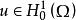 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理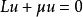 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理2. 存在非零的, 使得。
 弗雷德霍姆二擇一定理
弗雷德霍姆二擇一定理此外,使第二種情況成立的μ是離散的,只能以為極限點,對每一特徵值μ,相應的特徵函式空間是有限維的 。

