製作方法
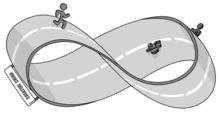莫比烏斯圈拿一張白的長紙條，把一面塗成黑色，然後把其中一端翻一個身，粘成一個莫比烏斯帶。用剪刀沿紙帶的中央把它剪開。紙帶不僅沒有一分為二，反而剪出一個兩倍長的紙圈。
新得到的這個較長的紙圈，本身卻是一個雙側曲面，它的兩條邊界自身雖不打結，但卻相互套在一起。把上述紙圈，再一次沿中線剪開，這回可真的一分為二了，得到的是兩條互相套著的紙圈，而原先的兩條邊界，則分別包含於兩條紙圈之中，只是每條紙圈本身並不打結罷了。
相反，拿一張白的長紙條，把一面塗成黑色，反方向把其中一端翻一個身，粘成一個莫比烏斯帶。用剪刀沿紙帶的中央把它剪開。紙帶不僅沒有一分為二，反而剪出兩個環套環的莫比烏斯帶。
即;莫比烏斯帶沿著中間剪開，可以得到一個一個兩倍長的紙圈，也可得到兩個環套環的莫比烏斯帶。
莫比烏斯帶還有更為奇異的特性。一些在平面上無法解決的問題，卻不可思議地在莫比烏斯帶上獲得了解決。
比如在普通空間無法實現的"手套易位"問題：人左右兩手的手套雖然極為相像，但卻有著本質的不同。我們不可能把左手的手套貼切地戴到右手上去；也不能把右手的手套貼切地戴到左手上來。無論你怎么扭來轉去，左手套永遠是左手套，右手套也永遠是右手套！不過，倘若你把它搬到莫比烏斯帶上來，那么解決起來就易如反掌了。
在自然界有許多物體也類似於手套那樣，它們本身具備完全相像的對稱部分，但一個是左手系的，另一個是右手系的，它們之間有著極大的不同。
和幾何學關係
可以用參數方程式創造出立體莫比烏斯帶（如右下圖）
這個方程組可以創造一個邊長為1半徑為1的莫比烏斯帶，所處位置為 x-y面，中心為（0，0，0）。參數
u在 v從一個邊移動到另一邊的時候環繞整個帶子。
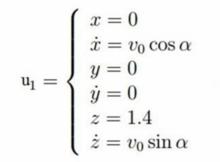莫比烏斯帶的參數方程從拓撲學上來講，莫比烏斯帶可以定義為矩陣[0,1]×[0,1]，邊由在0≤ x≤1的時候（ x,0）~（ 1-x,1）決定。
莫比烏斯帶是一個二維的緊緻流形（即一個有邊界的面），可以嵌入到三維或更高維的流形中。它是一個不可定向的的標準範例，可以看作 RP# RP。同時也是數學上描繪纖維叢的例子之一。特別地，它是一個有一纖維單位區間， I= [0,1]的圓 S上的非平凡叢。僅從莫比烏斯帶的邊緣看去給出 S上一個非平凡的兩個點（或 Z）的從。
拓撲變換
莫比烏斯帶是一種拓展圖形，它們在圖形被彎曲、拉大、縮小或任意的變形下保持不變，只要在變形過程中不使原來不同的點重合為同一個點，又不產生新點。換句話說，這種變換的條件是：在原來圖形的點與變換了圖形的點之間存在著一一對應的關係，並且鄰近的點還是鄰近的點。這樣的變換叫做拓撲變換。拓撲有一個形象說法——橡皮幾何學。因為如果圖形都是用橡皮做成的，就能把許多圖形進行拓撲變換。例如一個橡皮圈能變形成一個圓圈或一個方圈。但是一個橡皮圈不能由拓撲變換成為一個阿拉伯數字8。因為不把圈上的兩個點重合在一起，圈就不會變成8，“莫比烏斯帶”正好滿足了上述要求。
旋轉緯度的分析
傳統的三維世界裡，所有的維度都是直線式的，但如果將旋轉視為一種緯度，則相對容易對莫比烏斯帶進行解釋。
從莫比烏斯帶的結構來看，它包含了一個水平360度旋轉的維度，同時包含了一個垂直方向上360度旋轉的維度，加上帶子本身的平面（x,y）維度，莫比烏斯帶總共是四個維度。
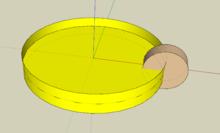兩個旋轉緯度的關係如果垂直方向上旋轉的度數繼續增加，只會增加莫比烏斯帶纏繞的圈數，並不會額外增加空間的維度。
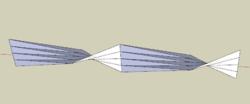垂直方向上增加維度的示意趣味數學
| 趣味數學以帶有強烈的遊戲色彩知名於世。歐拉就是通過對bridge-crossing之謎的分析打下了拓撲學的基礎。萊布尼茨也寫到過他在獨自玩插棍遊戲時分析問題的樂趣。希爾伯特證明了切割幾何圖形中的許多重要定理。馮·紐曼奠基了博弈論。最受大眾歡迎的計算機遊戲—生命是英國著名數學家康威發明的。愛因斯坦也收藏了整整一書架關於數學遊戲和數學謎的書。 |
