排隊系統的組成和特徵
一般的排隊系統都有三個基本組成部分:(1)輸人過程;(2)排隊規則;(3)服務機構。
下面分別說明各部分的特徵 。
輸人過程
輸人即指顧客到達排隊系統,可能有下列各種不同情況,當然這些情況並不是彼此排斥的。
(1) 顧客總體(稱為顧客源)的組成可能是有限的,也可能是無限的。猶如上遊河水流人水庫,可以認為總體是無限的,工廠內停機待修的機器顯然是有限的總體。
(2) 顧客到來的方式可能是一個一個的,也可能是成批的。例如,到餐廳就餐就有單個到來的顧客和受邀請來參加宴會的成批顧客。
(3) 顧客相繼到達的間隔時間可以是確定型的,也可以是隨機型的。例如,在自動裝配線上裝配的各部件就必須按確定的時間間隔到達裝配點,定期運行的班車、班輪、班級的到達也都是確定型的。但一般到商店購物的顧客、到醫院診病的病人、通過路口的車輛等,他們(或它們)的到達都是隨機型的。對於隨機型的情形,要知道單位時間內的顧客到達數或相繼到達的間隔時間的機率分布。
(4) 顧客的到達可以是相互獨立的,也就是說,以前的到達情況對以後顧客的到來沒有影響,否則就是有關聯的。例如,工廠內的機器在一個短的時間區間內出現停機(顧客到達)的機率就受已經待修或被修理的機器數目的影響。
(5) 輸人過程可以是平穩的,或是對時間齊次的,是指描述相繼到達的時間間隔分布和所含參數(如期望值,方差等)都是與時間無關的,否則成為非平穩的。非平穩情形的數學處理很困難。
排隊規則
(1) 顧客到達時,如所有服務台都正被占用,在這種情形下顧客可以隨即離去,也可以排隊等候。隨即離去的稱為即時制或稱損失制,因為這將失掉許多顧客;排隊等候的稱為等待制。普通市內電話的呼喚屬於前者,而登記市外長途電話的呼喚屬於後者。對於等待制,為顧客進行服務的次序可以採用下列各種規則:先到先服務、後到先服務、隨機服務、有優先權的服務等。
先到先服務,即按到達次序接受服務,這是最通常的情形。
後到先服務,如乘用電梯的顧客常是後人先出的。倉庫中存放的厚鋼板也是如此。在情報系統中,最後到達的信息往往是最有價值的,因而常採用後到先服務(指被採用)的規則。
隨機服務,指服務員從等待的顧客中隨機選取其一進行服務,而不管到達的先後,如電話交換台接通呼喚的電話就是如此。
有優先權的服務,如醫院對於病情嚴重的患者將給予優先治療。
(2) 從占有的空間來看,佇列可以排在具體的處所(如售票處、候診室等),也可以是抽象的(如向電話交換台要求通話的呼喚)。由於空間的限制或其他原因,有的系統要規定容量(即允許進人排隊系統的顧客數)的最大限制;有的沒有這種限制(即認為容量可以是無限的)。
(3) 從佇列的數目看,可以是單列,也可以是多列。在多列的情形,各列間的顧客有的可以互相轉移,有的不能(如用繩子或欄桿隔開)。有的排隊顧客因等候時間過長而中途退出,有的不能退出(如高速公路上的汽車流),必須堅持到被服務為止。
服務機構
從機構形式和工作情況來看有以下五種情況。
(1) 服務機構可以沒有服務員,也可以有一個或多個服務員(服務台、通道、視窗等)。例如,在敞架售書的書店,顧客選書時就沒有服務員,但交款時可能有多個服務員。
(2) 在有多個服務台的情形中,它們可以是平行排列(並列)的,可以是前後排列(串列)的,也可以是混合的。
(3) 服務方式可以對單個顧客進行,也可以對成批顧客進行,公共汽車對在站台等候的顧客就屬於成批進行服務。
(4) 和輸人過程一樣,服務時間也分確定型的和隨機型的。自動沖洗汽車的裝置對每輛汽車沖洗(服務)的時間就是確定型,但大多數情形的服務時間是隨機型的。對於隨機型的服務時間,需要知道機率分布。
如果輸人過程,即相繼到達的間隔時間,和服務時間都是確定型,那么問題就太簡單了,因此,在排隊論中所討論的是二者至少有一個是隨機型的情形 。
排隊模型的概述
排隊系統的主要數量指標
研究排隊系統的主要目的是通過了解系統運行的狀況,對系統進行調整和控制,使系統處於最優運行狀態。因此,首先需要弄清系統的運行狀況。描述一個排隊系統運行狀況的主要數量指標有:
隊長和佇列長(排隊長)。隊長是指系統中的顧客數(排隊等待的顧客與正在接受服務的顧客數之和);佇列長是指系統中正在排隊等待服務的顧客數。隊長和佇列長般都是隨機變數。隊長的分布是顧客和服務員都關心的;特別是對系統設計人員來說,如果能知道隊長的分布,就能確定隊長超過某個數的機率,從而確定合理的等待空間。
等待時間和逗留時間。從顧客到達時刻起到開始接受服務止的這段時間稱為等待時間。等待時間是個隨機變數,也是顧客最關心的指標,因為顧客通常是希望等待時間越短越好。從顧客到達時刻起到他接受服務止的這段時間稱為逗留時間,也是隨機變數,顧客同樣非常關心。
忙期和閒期。忙期是指從顧客到達空閒著的服務機構起,到服務機構再次成為空閒止的這段時間,即服務機構連續忙的時間。這是個隨機變數,是服務員最為關心的指標,因為它關係到服務員的服務強度。與忙期相對的是閒期,即服務機構連續保持空閒的時間。在排隊系統中,忙期和閒期是交替出現的。
除了上述幾個基本數量指標外,還會用到其他一些重要指標。例如,在損失制或系統容量有限的情況下,由於顧客被拒絕,而使服務系統受到損失的顧客損失率及服務強度等,也都是十分重要的指標 。
排隊系統的符號表示
D.G.Kendall 於1953年提出一個分類方法,按照上述各部分的特徵中最主要的、影響最大的三個分類:(1)相繼顧客到達間隔時間的分布;(2)服務時間的分布;(3)服務台個數。
按照這三個特徵分類,並用一定符號表示,稱為 Kendall 記號。這僅對並列的服務台(如果服務台多於1個的話)的情形,用的符號形式為
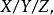 排隊過程
排隊過程其中X處填寫表示相繼到達間隔時間的分布,Y 處填寫表示服務時間的分布,Z處填寫並列的服務台的數目。
表示相繼到達間隔時間和服務時間的各種分布的符號如下:
 排隊過程
排隊過程——負指數分布(M是Markov的字頭,因為負指數分布具有無記憶性,即Markov性);
 排隊過程
排隊過程—— 確定型;
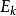 排隊過程
排隊過程—— k階愛爾朗(Erlang)分布;
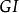 排隊過程
排隊過程—— 一般相互獨立(general independent)的時間間隔的分布;
 排隊過程
排隊過程——一般服務時間的分布。
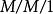 排隊過程
排隊過程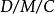 排隊過程
排隊過程例如,表示相繼到達間隔時間為負指數分布、服務時間為負指數分布、單服務台的模型;表示確定的到達間隔、服務時間為負指數分布、C個平行服務台(但顧客是一隊)的模型。
1971年,一次關於排隊論符號標準化會議,將Kendall 符號擴充為
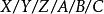 排隊過程
排隊過程形式,其中前項意義不變,而A處填寫系統容量限制N,B處填寫顧客源數目m,C處填寫服務規則,如先到先服務FCFS、後到先服務LCFS等。
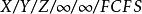 排隊過程
排隊過程同時約定,如略去後三項,即指的情形 。

