概述
如果任務到達的速度超過服務的速度,就會出現排隊現象,當指的是到達速度的平均值超過服務速度的平均值時,這種排隊是不穩定的。但即使平均講服務速度比到達速度高,仍然會有可能排隊:這是因為,任務的到達是隨機的,服務時間也是隨機變化的,所以在某段時間內·,到達的速度仍有可能超過服務的速度,當然,在這種情況下,隊伍的長度經常只在有限範圍內變動,我們稱這種排隊是穩定的 。
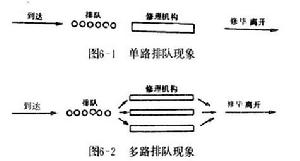 排隊模型
排隊模型多路排隊
多路排隊(multiple queue)是指在多通道服務系統中,每個通道各排成一個隊等待通道服務的排隊系統。每個通道只為相對應的一隊車輛服務,車輛不能隨意換隊,這種情況相當於N個單通道服務系統。
排隊論
排隊論是研究“服務”系統因“需求”擁擠而產生等待行列即排隊的現象,以及合理協調需求與服務關係的一種數學理論,是運籌學中以機率論為基礎的一門重要分支,亦稱“隨機服務系統理論”。
排隊論是20世紀初開始發展的。1905年丹麥哥本哈根電話工程師愛爾朗首先在電話自動交換機設計時套用排隊論。使電話機既能滿足通話需求而又不致設線過多。第二次世界大戰以後,排隊論在很多領域內被採用。在交通工程中,對於研究車輛延誤、通行能力、信號燈配時以及停車場、加油站等交通設施的設計與管理方面得到廣泛的套用。
1936年亞當斯( Adams.W.F)用以考慮未設定交通信號交叉口的行人延誤問題,1951年唐納予以推廣套用,1954年伊迪(Edie)套用排隊模型估計收費亭的延誤。同年在摩斯柯維茨的報告中,將其套用於車輛等候交通流空檔的實驗報告 。
排隊系統
排隊系統的3個組成部分:輸入、排隊、輸出。
(1)輸入過程就是指各種類型的“顧客(車輛或行人)”按怎樣的規律到達。有各式各樣的輸入過程,例如:
定長輸入:顧客等時距到達;
泊松輸入:顧客到達時距符合負指數分布。這種輸入過程最容易處理,因而套用最廣泛;
愛爾朗輸入:顧客到達時距符合愛爾朗分布。
(2)排隊(規則)指到達的顧客按怎樣的次序接受服務,例如:
損失制:顧客到達時,若所有服務台均被占,該顧客就自動消失,永不再來。
等待制:顧客到達時,若所有服務台均被占,他們就排成隊伍,等待服務,服務次序有先到先服務(這是最通常的情形)和優先權服務如急救車、消防車優先)等多種規則。
混合制:顧客到達時,若隊伍長小於L,就排入隊伍,若隊伍長等於L,顧客就離去,永不再來。
(3)服務方式(輸出)指同一時刻有多少服務台可接納顧客,每一顧客服務了多少時間。每次服務可以接待單個顧客,也可以成批接待,例如公共汽車一次就裝載大批乘客 。

