基本定義
在做排列的題目時,經常會遇到題乾要求兩個或多個元素必須相鄰。針對這類題型,可以把這幾個相鄰的元素捆綁在一起,作為一個整體來考慮。這類題目基本都是 排列問題,需要注意捆綁後內部元素之問的排列。
注意點
運用捆綁法解決排列組合問題時,一定要注意“捆綁”起來的大元素內部的順序問題,見下文例題。
例題解析
例1 某領導小組共7人合影留念,要求甲領導和乙領導必須站在一起,那么一共有多少種不同的排法?
A.200 B.240 C.360 D.720 E.1440
【答案】 E
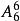 捆綁法
捆綁法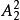 捆綁法
捆綁法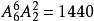 捆綁法
捆綁法【解析】甲與乙必須站在一起,將甲和乙“捆綁”在一起,看做一個人,與剩下的5個人組成6的全排列。但是這裡面要注意的是甲、乙兩者之間的順序,即甲在乙左邊和甲在乙右邊是不同的排法,所以甲乙內部有個2的全排列種排法。所以一共有種不同的排法。答案選E。
例2 某市舉辦經濟建沒成就展,計畫在六月上旬組織5個單位參觀,其中1個單位由於人數較多,需要連續參觀2天。其他4個單位只需參觀1天,若每天最多只能安排一個單位參觀,則參觀的時間安排共有( )種。
A.630 B.700 C.15120 D.16800
【答案】C
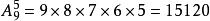 捆綁法
捆綁法【解析】六月上旬有10天,把需要連續參觀的2天捆綁視為一個整體,本題相當於從9天中取5天進行全排列,種。
例3 一排9個座位坐了3個三口之家,若每家人坐在一起,則不同的坐法種數為( )。
A.3x3! B.3x(3!) C.(3!) D.9!
【答案】C
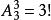 捆綁法
捆綁法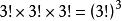 捆綁法
捆綁法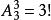 捆綁法
捆綁法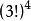 捆綁法
捆綁法【解析】先把三個家庭分別排列,每個家庭有種排法,三個家庭共有種排法;再把三個家庭進行全排列有種排法,因此不同的坐法種數為,選C。

