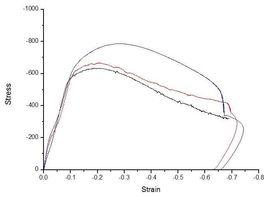
簡介
應變率是材料相對於時間的應變(變形)的變化,其定義由美國冶金學家Jade LeCocq於1867年首次引入,其定義為“應變發生率,是應變變化的時間率”。 在物理學中,應變速率通常被定義為應變相對於時間的導數。 其精確定義取決於應變如何測量。應變率是表征材料變形速度的一種度量,應變對時間的導數,高應變率下納晶能獲得更高的強度和更好的韌性,但是材料的彈性模量並不受此影響。
材料中某一點的應變率測量材料的相鄰的距離隨著時間在該點附近的速率變化。它既包括材料膨脹或收縮的速率(膨脹率),也包括其逐漸剪下變形的速率,而不改變其體積(剪下速率)。如果這些距離沒有改變,則為零,如同某個區域中的所有顆粒以相同的速度(相同的速度和方向)移動和/或以相同的角速度旋轉時發生的,就好像該部分介質是剛性的身體。
應變率是材料科學和連續力學的概念,在流體和可變形固體的物理學中起著至關重要的作用。在各向同性牛頓流體中,特別是粘性應力是由兩個係數定義的應變速率的線性函式,一個與膨脹率(體積粘度係數)有關,一個與剪下速率有關(“普通” “粘度係數”)。
研究材料動態力學性能的系列實驗按應變率大小排列有:中應變率實驗(10E0~10E2/s)、高應變率實驗(10E2~10E4/s)、超高應變率實驗(10E4~10E6/s)。
材料的性能受應變率影響很大,但是傳統粗晶材料對應變率並不敏感,而納米材料卻並非如此。具體機制不同文獻解釋不同,但是總起來說尚沒有統一的認識。
簡單變形
在簡單的環境中,單個數字可能足以描述應變,因此描述應變速率。 例如,當長而均勻的橡膠帶通過在端部處拉伸而逐漸拉伸時,應變可以被定義為拉伸量與帶的原始長度之間的比率,
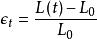 應變率
應變率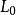 應變率
應變率其中是原始長度,L(t)是每個時間t的長度。 那么應變率就是,
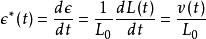 應變率
應變率其中v(t)是端部彼此遠離的速度。
當材料經受平行剪下而不改變體積時,應變速率也可以由單數表示;即當變形可以被描述為一組無窮小的平行層,如同它們是剛性片一樣在相同的方向上彼此滑動,而不改變它們的間距。 該描述適用於平行於彼此滑動的兩個實心板之間的流體層流(Couette流)或恆定橫截面(Poiseuille流)的圓形管內。在這些情況下,由於任意的開始時間,可以通過每層的位移X(y,t)來描述材料在某個時間 t的狀態,作為其距離固定牆的距離y的函式。那么每個層中的應變可以表示為當前相對位移X(y + d,t)-X( y,t)除以層之間的間距d,
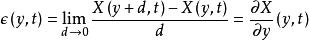 應變率
應變率因此,應變率為:
 應變率
應變率其中V(y,t)是距離牆壁距離為y的材料的當前線速度。
應變率張量
在更一般的情況下,當材料以不同的速率在各個方向上變形時,材料內的點周圍的應變(因此應變速率)不能由單個數量或甚至單個向量表示。在這種情況下,變形率必須用張量表示,矢量之間的線性映射,表示當一個移動距離給定方向上的點一小段距離時介質的相對速度如何變化。該應變率張量可以定義為應變張量的時間導數,或者定義為材料速度的梯度(相對於位置的導數)的對稱部分。
使用選定的坐標系,應變率張量可以由實數的對稱3×3矩陣表示。應變率張量通常隨著材料內的位置和時間而變化,因此是(時變)張量場。它只描述了當地的一階變形速率;但是對於大多數目的來說,這通常是足夠的,即使當材料的粘度高度非線性時也是如此。
單位
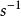 應變率
應變率應變基本上是兩個長度的比例,因此它是一個無量綱的數量(不依賴於測量單位的選擇)。 因此,應變率在尺寸上是時間的倒數。 在國際單位制(SI)中,以秒()的倒數進行測量。