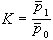粘塑性理論
正文
考慮固體材料粘性的塑性理論(見塑性力學)。固體粘性是指與時間有關的變形性質，蠕變和應力鬆弛都是與粘性有關的力學現象。幾乎所有固體材料都有粘性。有些情況下，粘性對材料力學性能的影響小到可以忽略，但某些聚合物、岩土材料以及處於高速變形狀態下的金屬材料則具有明顯的粘性。對於這些材料和變形情況，粘性的影響必須予以考慮。實驗表明，同時考慮材料的塑性和粘性，對於描述應力波的傳播和在短時強載荷作用下結構的動力特性是非常必要的。在這些問題中，考慮材料的粘性效應能使計算結果的實驗數據比較接近。具有塑性和粘性的物體稱為粘塑性體。在粘塑性理論的本構關係中，要考慮應變率效應。最早研究粘塑性體並給出簡單力學模型的是美國的E.C.賓厄姆。他給出了單向應力狀態下粘塑性體的本構關係，即
σ＝σY+μ夊當σ>σY，
式中μ為粘性係數；夊為應變率；σY為材料的屈服極限。當σ≤σY時，物體不會產生變形。用上式描述本構關係的物體稱為賓厄姆體，其力學模型如圖所示。這種模型實際上是理想剛塑性體和牛頓流體的組合。賓厄姆體不同於流體的是它具有不可恢復的塑性變形，所以它仍屬於固體材料。 對於粘塑性材料，屈服條件不僅同應力、塑性應變和強化性質有關，而且還同反映材料粘性的參數有關。美國的L.E.馬爾文曾給出了考慮應變率效應的本構關係。 他假設實際應力與靜力應力-應變曲線上的應力之差同塑性應變率成正比，該應力差引起按粘性規律變化的應變率效應。他所提出的本構關係的形式可寫為：
，
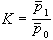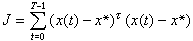中的函式；ф【σ-g(ε)】為由實驗確定的函式；符號< >按下式定義：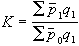 
波蘭的P.佩日納根據金屬材料的動力實驗結果，在考慮應變率對材料屈服條件影響的基礎上，給出了能反映粘塑性材料動力特性的本構方程：
，
式中妏ij、妡ij分別為應變率偏量和應力率偏量（即應變偏量和應力偏量對時間的變率）;γ為控制塑性流動速度的粘性係數；G為剪下模量；f為屈服函式（見屈服條件）；F為反映複雜應力狀態下動力特性的參量;函式ф(F)應根據材料動力實驗結果確定。分析粘塑性理論中的準靜力學問題和研究塑性力學中的問題相似，採用線性化的屈服函式和剛粘塑性模型，可以得到梁、圓板、球體等簡單問題的解析解。對於簡支圓板，粘塑性問題的分析結果與實驗數據很接近。但對於幾何形狀、支承條件和載荷情況比較複雜的結構，只能用數值計算方法尋求近似解。
近年來所發展的基於位錯動力學的博德 -帕頓理論，也較好地反映了固體材料的粘塑性性質。該理論的特點是，不需要引進屈服函式和載入與卸載準則，在套用上比較方便。
