簡介
固體力學的一個研究內容。它在考慮材料的彈性性質和粘性性質的基礎上,研究材料內部應力和應變的分布規律以及它們和外力之間關係。材料的粘性性質主要表現為材料中的應力和應變率有關。
詳解
黏彈體可以理解為是彈性體與液體的混合物。在黏彈體發生應變的時候,其中的彈性部分承擔靜態的應力,而液體部分不承擔靜態的應力。當應變對時間的導數不為零的時候,液體部分由於存在微觀摩擦,出現黏度,而承擔動態的應力。因此,一個靜態的黏彈體與一個純彈性體相當。
而靜態的水的內部沒有任何剪下應力,這是黏彈體的一個極限。純粹的彈性體在發生應變隨時間變化的過程中,沒有黏度,應變不滯後於應力,這是黏彈體的另一個極限。因此黏彈體是介乎於固體與液體之間的凝聚體。
有不少工程材料,如混凝土、高聚合材料、某些生物組織以及處於高速變形狀態的金屬材料,既具有彈性性質,又具有粘性性質,這種兼具彈性性質和粘性性質的材料稱為粘彈性體。在外力作用下,粘彈性體產生彈性變形,而且變形還隨時間而變化,因此用彈性力學方法來研究粘彈性體就不能反映實際情況。粘彈性理論與彈性力學的主要區別在於應力-應變關係不同。因此,粘彈性體的應力-應變關係就成為粘彈性理論的主要研究內容。
 粘彈性理論
粘彈性理論通常用服從胡克定律的彈性元件和服從牛頓粘性定律(即應力和應變率成正比)的粘性元件來表征粘彈性體的特性。用這兩種元件的不同組合模型可以反映多種複雜粘彈性體的應力-應變關係。兩種最基本的粘彈性體模型是麥克斯韋模型和開爾文模型。前者為彈
性元件和粘性元件串聯 (圖中的a),它的總應變是彈性應變和粘性應變之和,對應的本構方程為:
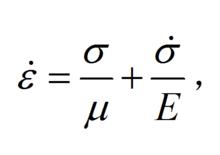 粘彈性理論
粘彈性理論 粘彈性理論
粘彈性理論式中點為應變率,即應變 ε對時間的導數; μ為粘性元件的粘性係數; E為彈性元件的彈性模量(見材料的力學性能; σ和 σ點分別為應力和應力率。後者為彈性元件和粘性元件並聯(圖中的b),其彈性伸長和粘性伸長相等,而總應力為彈性應力和粘性應力之和,對應的本構方程為:
 粘彈性理論
粘彈性理論上述兩方程還可推廣到複雜應力狀態問題。在實際中,常需將多個彈性元件和粘性元件按各種不同形式串聯或並聯,以描述不同粘彈性體的特性。
粘彈性理論中的幾何方程和運動方程與彈性力學完全相同。從理論上說,利用本構方程、運動方程、幾何方程、邊界條件以及初始條件,可找到粘彈性邊值問題的解。在緩慢載入的前提下,如果粘彈性體所受的體積力、表面力和粘彈性體的位移邊界條件都可以寫成空間和時間的分離變數形式,且全部應力、應變以及它們對時間的各階導數的初始值都為零,則可利用對時間的拉普拉斯變換,把一個線性粘彈性體的問題化為一個同樣形狀和大小的線性彈性體的問題。求出後者的解並利用拉普拉斯逆變換,就能得到原粘彈性體問題的解。
各種材料的粘彈性性能,可通過蠕變實驗和振動實驗加以確定。
