概述
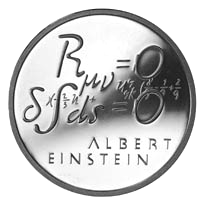刻上真空場方程式的紀念硬幣1.愛因斯坦場方程：
R_uv-1/2*R*g_uv=κ*T_uv
（Rμν-（1/2）gμνR=8GπTμν/（c*c*c*c） -gμν）
說明：g_uv為度規，κ為係數，可由低速的牛頓理論來確定。"_"後字母為下標，"^"後字母為上標。
意義：空間物質的能量-動量（T_uv）分布=空間的彎曲狀況（R_uv）
解的形式是：ds^2=Adt^2+Bdr^2+Cdθ^2+Ddφ^2
式中A,B,C,D為度規g_uv分量。
考慮能量－動量張量T_uv的解比較複雜。最簡單的就是讓T_uv等於0，對於真空靜止球對稱外部的情況，則有施瓦西外解。如果是該球體內部的情況，或者是考慮球體軸對稱的鏇轉，就稍微複雜一點。還有更複雜的星雲內部或外部的情況，星雲內部的星球還要運動、轉動等。這些因素都要影響到星雲內部的曲面空間。
2.含宇宙常數項的場方程：
R_uv-1/2*R*g_uv+Λ*g_uv=κ*T_uv
此處的Λ是宇宙常數，其物理意義是宇宙真空場。Λ*g_uv為宇宙項。
如果從數學上理解的話，則上面的場方程也可解出下面的形式：
ds^2=Adt^2+Bdr^2+Cdθ^2+Ddφ^2
式中A,B,C,D為度規g_uv分量。
這裡的ds就是表達空間彎曲程度的一小段距離。同時因為4維空間與時間有關，ds隨時間也會變化。這時，如果沒有宇宙項，ds隨時間是增大的，宇宙就是膨脹的。如果加了宇宙項，選取適當的Λ值，ds不隨時間變化，宇宙就是穩定的。
如果從物理意義上理解的話，把宇宙項移到式右邊，則是：
R_uv-1/2*R*g_uv=κ*T_uv-Λ*g_uv
Λ項為負值，起到了斥力的作用，即宇宙真空場與普通物質場之間存在著斥力。宇宙項和通常物質場的引力作用起到了平衡的作用，所以可得到穩定的宇宙解。
性質
非線性
愛因斯坦場方程的非線性特質使得廣義相對論與其他物理學理論迥異。舉例來說，電磁學的麥克斯韋方程組跟電場、磁場以及電荷、電流的分布是呈線性關係（亦即兩個解的線性疊加仍然是一個解）。另個例子是量子力學中的薛丁格方程，對於機率波函式也是線性的。
對應原理
透過弱場近似以及慢速近似，可以從愛因斯坦場方程退化為牛頓重力定律。事實上，場方程中的比例常數是經過這兩個近似，以跟牛頓重力理論做連結後所得出。
