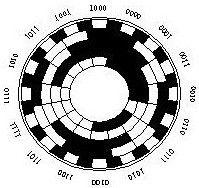
歷史
Gray Code是由貝爾實驗室的Frank Gray在20世紀40年代提出的(是1880年由法國工程師Jean-Maurice-EmlleBaudot發明的),用來在使用PCM(Pusle Code Modulation)方法傳送訊號時避免出錯,並於1953年3月17日取得美國專利。由定義可知,Gray Code的編碼方式不是唯一的,這裡討論的是最常用的一種。
原理
格雷碼屬於可靠性編碼,是一種錯誤最小化的編碼方式,因為,自然二進制碼可以直接由數/模轉換器轉換成模擬信號,但某些情況,例如從十進制的3轉換成4時二進制碼的每一位都要變,使數字電路產生很大的尖峰電流脈衝。而格雷碼則沒有這一缺點,它是一種數字排序系統,其中的所有相鄰整數在它們的數字表示中只有一個數字不同。它在任意兩個相鄰的數之間轉換時,只有一個數位發生變化。它大大地減少了由一個狀態到下一個狀態時邏輯的混淆。另外由於最大數與最小數之間也僅一個數不同,故通常又叫格雷反射碼或循環碼。
用例
下表為幾種自然二進制碼與格雷碼的對照表:
| 十進制數 | 自然二進制數 | 格雷碼 | 十進制數 | 自然二進制數 | 格雷碼 |
| 0 | 0000 | 0000 | 8 | 1000 | 1100 |
| 1 | 0001 | 0001 | 9 | 1001 | 1101 |
| 2 | 0010 | 0011 | 10 | 1010 | 1111 |
| 3 | 0011 | 0010 | 11 | 1011 | 1110 |
| 4 | 0100 | 0110 | 12 | 1100 | 1010 |
| 5 | 0101 | 0111 | 13 | 1101 | 1011 |
| 6 | 0110 | 0101 | 14 | 1110 | 1001 |
| 7 | 0111 | 0100 | 15 | 1111 | 1000 |
一般的,普通二進制碼與格雷碼可以按以下方法互相轉換:
二進制碼-〉格雷碼(編碼):從最右邊一位起,依次將每一位與左邊一位異或(XOR),作為對應格雷碼該位的值,最左邊一位不變(相當於左邊是0);
格雷碼-〉二進制碼(解碼):從左邊第二位起,將每位與左邊一位解碼後的值異或,作為該位解碼後的值(最左邊一位依然不變)。
數學(計算機)描述:
原碼:p[0~n];格雷碼:c[0~n](n∈N);編碼:c=G(p);解碼:p=F(c);書寫時從左向右標號依次減小.
編碼: c=p XOR p[i+1](i∈N,0≤i≤n-1),c[n]=p[n];
解碼: p[n]=c[n],p=c XOR p[i+1](i∈N,0≤i≤n-1).