簡介
階碼:對於任意一個二進制數N,可用N=S×2P表示,其中S為尾數,P為階碼,2為階碼的底,P、S都用二進制數表示,S表示N的全部有效數字,P指明小數點的位置。當階碼為固定值時,數的這種表示法稱為定點表示,這樣的數稱為“ 定點數”;當階碼為可變時,數的這種表示法稱為 浮點表示,這樣的數稱為“ 浮點數”,這在前面已有介紹。
定點數表示法
通常 定點數有兩種表示法,均設P=0,小數點是隱含的,若數值部分為n位:
當S為純 整數時,此時 定點數只能表示整數,所能表示的N範圍是(2n-1)≥N≥-(2n-1);當S為 純小數時,此時定點數只能表示小數,所能表示的N範圍是(1-2-n)≥N≥-(1-2-n)。
實際數值不一定都是純整數或 純小數,運算前可選擇比例因子,使所有原始數據化成純小數或純整數,運算後再用比例因子恢復成實際值。
比較特殊的編碼
1、BCD碼
2、階碼
3、移碼
BCD碼
通常,我們習慣用十進制數表示數據,但計算機是用二進制數來表示數據的,這就需要進行數值進制之間的轉換。我們把每位十進制數轉換二進制數的編碼,簡稱為BCD碼(BinaryCodedDecimal)。BCD編碼具有二進制數的形式以滿足數字系統的要求,又具有十進制數的特點。在某些情況下,計算機也可以對這種形式的數直接進行運算。
它是一種數字壓縮存儲編碼,一個位元組有8位,而數字0到9最多只需要使用4位,如果用一個位元組來存儲一個數字相對就會有一定的浪費,尤其是在傳輸過程中,由此人們就想出了壓縮的辦法,就是BCD編碼。
BCD編碼將一個位元組的8位拆分成高4位和低4位兩個部分,也就是說一個位元組能存儲兩個數字。所以BCD的編碼過程就是將數字壓縮的過程,將兩個位元組的數字壓縮成一個位元組。反之,解碼就是把一個位元組的數字拆分為兩個數字單獨存放(大部分的處理都是按位元組處理的)。
BCD碼使用4位二進制數編碼來表示1位十進制數(與十六進制數類似)。這種編碼方法有多種,常見的有以下幾種:
8421BCD編碼
這是一種使用最廣的BCD碼,是一種有權碼,其各位的權分別是(從最有效高位開始到最低有效位)8、4、2、1(即23、22、21、20),因而稱為“8421BCD編碼”。
在使用8421BCD碼時一定要注意其有效的編碼僅十個,即:0000~1001。4位二進制數的其餘6個編碼1010、1011、1100、1101、1110、1111不是有效編碼。8421BCD編碼如表2-3所示。這種BCD編碼實際上就是0~9的“等值”二進制數。
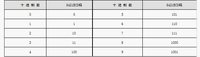 階碼
階碼2421BCD編碼
2421BCD碼也是一種有權碼,其從高位到低位的權分別為2、4、2、1(同樣也是它得名的原因),其也可以用4位二進制數來表示1位十進制數。
餘3碼
餘3碼也是一種BCD碼,但它是無權碼。但由於每一個碼對應的8421BCD碼之間相差3,故稱為餘3碼,其一般使用較少,故只須作一般性了解。
用BCD碼進行進制的轉換時,要求在兩種進制的表現形式上快速轉換,而不是要求在“數值相等”的含義快速轉換。
例如求十進制數2000的BCD編碼和其二進制數。
2000的BCD編碼是把每位上的數2、0、0、0分別轉換為其對應的BCD編碼:0010、0000、0000和0000,把它們合在一起就是2000的BCD編碼:0010000000000000。
十進制數2000的二進制數是:11111010000,它們在數值上是相等的。
將十進制數86.5轉換為BCD碼,最終的結果是:(10000110.0101)BCD。
將BCD碼10010111.0100轉換為十進制數的結果是:97.4。
在IBMPC機中,根據在存儲器中的不同存放格式,BCD碼又分為:
壓縮型BCD碼:一個位元組中存放兩個十進制數碼。
非壓縮型BCD碼:每個位元組只存放一個十進制數。
例如:將十進制數8762用壓縮型BCD碼錶示,則為:1000011101100010。
移碼
表示浮點數時還常用一種稱為移碼的碼制。浮點數的階碼錶示指數大小,有正有負,為避開階碼的符號,對每個階碼都加上一個正的常數(稱偏移常數),使能表示的所有階碼都為正整數,變成“偏移”了的階碼,又稱“增碼”。移碼的值不小於0,這樣階碼總為0,可以取消,浮點數小數點的實際位置由移碼減去偏移常數來決定。
一個實數可表示成一個 純小數與一個 乘冪之積。如 ;-0.0010011=-0.10011×2^-10(10在這裡也是二進制);-110001101=-0.110001101×2^1001(1001同樣為二進制)。
一個任意 實數,在計算機內部可以用指數(為整數)和 尾數(為 純小數)來表示,用指數和尾數表示實數的方法稱為 浮點表示法。
浮點數的長度可以是32位、64位甚至更長,分階碼和 尾數兩部分。階碼位數越多,可表示的數的範圍越大;尾數越多,所表示的數的精度越高。“ 移碼”用來表示浮點型 小數的階碼。對於 正數,符號位為“1”,其餘位不變,如+1110001的階碼為11110001;對於 負數,符號位為“0”,其餘位取反,最後加“1”,如–1110001的階碼為00001111。
移碼與 補碼的關係是符號位互為 反碼,例如:X=+1011時,[X]移=11011,[X]補=01011;X=–1011時,[X]移=00101,[X]補=10101。
注意:對 移碼運算的結果需要加以修正,修正量為2n,即對結果的符號位取反後才是移碼形式的正確結果。 移碼錶示中,0有唯一的編碼——1000…00,當出現000…00時(表示–2n),屬於浮點數下溢。

