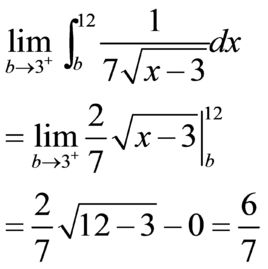廣義積分

定積分概念的推廣至分區間無窮和被積函式在有限區間上為無界的情形成為廣義積分，又名反常積分。其中前者稱為無窮限廣義積分，或稱無窮積分；後者稱為無界函式的廣義積分，或稱瑕積分。

瑕積分

設函式f(x)定義在[a,b)上，而f(x)在x=b的任一左鄰域內f(x)無界（此時稱x=b為f(x)的瑕點）。若f(x)在任意[a,b-ε](0<ε>

類似可定義a為瑕點時的瑕積分。

又設c∈(a,b),函式f(x)以點c為暇點，那么當兩個反常積分∫(a → c) f(x)dx和∫(c → b) f(x)dx均收斂時，反常積分∫(a → b) f(x)dx收斂。其值定義為：

∫(a → b) f(x)dx=∫(a → c) f(x)dx+∫(c → b) f(x)dx

=lim(ε →0+)∫[a→c-ε] f(x)dx+lim(ε →0+)∫[c+ε →b] f(x)dx,

否則該反常積分發散