模型定義
蛛網模型的基本假定是:商品的本期產量Qts決定於前一期的價格Pt-1,即供給函式為Qts=f(Pt-1),商品本期的需求量Qtd決定於本期的價格Pt,即需求函式為Qtd=f(Pt)。根據以上的假設條件,蛛網模型可以用以下三個聯立的方程式來表示:
Qtd=α-β·Pt
Qts=-δ+γ·Pt-1
Qtd=Qts
其中,α、β、δ和γ均為常數且均大於零。
 蛛網模型
蛛網模型由於區別了經濟變數的時間先後,因此,蛛網模型是一個動態模型。
數學推導
Qtd=α-β·Pt
Qts=-δ+γ·Pt-1
Qtd=Qts
三個方程聯立得
Pt=(α+δ)/β-(γ/β)Pt-1
Pt-1疊代後得
Pt=(α+δ)/β∑(-γ/β)^i+(-γ/β)^t·P0
即
Pt=[1-(-γ/β)^t](α+δ)/(β+γ)+(-γ/β)^t·P0(*)
詳細介紹
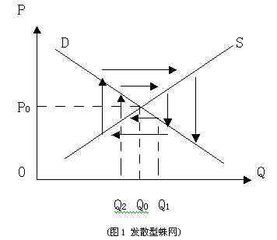
收斂型蛛網
供給彈性<需求彈性,或,供給曲線斜率絕對值>需求曲線斜率絕對值,此時即(*)中(-γ/β)^t一項趨於0,Pt趨於(α+δ)/(β+γ)。因為需求彈性大,表明價格變化相對較小,進而由價格引起的供給變化則更小,再進而由供給引起的價格變化則更小
相對於價格軸(注意:這裡是把Y軸作為參考軸系討論的,下文所說的“斜率‘”陡峭“都是以價格軸為參考軸而言的,與我們正常數學上以X軸為參考軸不同),需求曲線斜率的絕對值大於供給曲線斜率的絕對值。當市場由於受到干擾偏離原有的均衡狀態以後,實際價格和實際產量會圍繞均衡水平上下波動,但波動的幅度越來越小,最後會回復到原來的均衡點。
假定,在第一期由於某種外在原因的干擾,如惡劣的氣候條件,實際產量由均衡水平Qe減少為Q1。根據需求曲線,消費者願意支付P1的價格購買全部的產量Q1,於是,實際價格上升為P1。根據第一期的較高的價格水平P1,按照供給曲線,生產者將第二期的產量增加為Q2。
在第二期,生產者為了出售全部的產量Q2,接受消費者所願意支付的價格P2,於是,實際價格下降為P2。根據第二期的較低的價格水平P2,生產者將第三期的產量減少為Q3。
在第三期,消費者願意支付P3的價格購買全部的產量Q3,於是,實際價格又上升為P3。根據第三期的較高的價格水平P3,生產者又將第四期的產量增加為Q4。
如此循環下去,如前圖所示,實際產量和實際價格的波動的幅度越來越小,最後恢復到均衡點E所代表的水平。
由此可見,圖中的均衡點E所代表的均衡狀態是穩定的。也就是說,由於外在的原因,當價格和產量偏離均衡數值(Pe和Qe)後,經濟制度中存在著自發的因素,能使價格和產量自動地恢復均衡狀態。在圖中,產量和價格變化的途徑形成了一個蜘蛛網似的圖形,這就是蛛網模型名稱的由來。
在這裡,我們看到,除第一期受到外在原因干擾外,其它各期都不會再受新的外在原因干擾,從而前一期的價格能夠唯一決定下一期的產量。
按照動態的邏輯順序,我們還看到,生產者錯誤地根據上一期的價格決定供給量,消費者被動地消費生產者提供的全部生產量,而價格則由盲目生產出來的數量所決定。
在圖中,供求曲線各自只畫了一條,但是,經濟學在前面已經指出,供給的變動,不僅是指供給量沿著既定供給曲線的變動,還包括供給曲線的變動。需求的變動亦是如此。
那么,經濟學又是如何保證供求曲線在多個時期里,不受外在原因的干擾和盲目決策的影響,始終保持不變呢?而如果供求曲線本身也會隨著時期的不同而移動,那么,又如何保證蛛網是收斂型的呢?
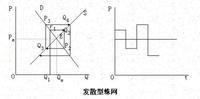
發散型蛛網
供給彈性>需求彈性,或,供給曲線斜率絕對值<需求曲線斜率絕對值,此時即(*)中(-γ/β)^t一項趨於無窮,Pt趨於發散。
相對於價格軸,需求曲線斜率的絕對值小於供給曲線斜率的絕對值。當市場由於受到外力的干擾偏離原有的均衡狀態以後,實際價格和實際產量上下波動的幅度會越來越大,偏離均衡點越來越遠。其原有的均衡狀態是不穩定的。
這種情況意味著產量可以無限供給,價格可以無限提高。
穩定型蛛網
供給彈性=需求彈性,或供給曲線斜率的絕對值等於需求曲線斜率的絕對值,此時即(*)中(-γ/β)^t一項=±1。
當市場由於受到外力的干擾偏離原有的均衡狀態以後,實際產量和實際價格始終按同一幅度圍繞均衡點上下波動,既不進一步偏離均衡點,也不逐步地趨向均衡點1。
價值
西方經濟學家認為,蛛網模型解釋了某些生產周期較長的商品的產量和價格的波動的情況,是一個有意義的動態分析模型。但是,這個模型還是一個很簡單的和有缺陷的模型。這是因為,根據該模型分析,造成產量和價格波動的主要原因是:生產者總是根據上一期的價格來決定下一期的產量,這樣,上一期的價格同時也就是生產者對下一期的預期價格。而事實上,在每一期,生產者只能按照本期的市場價格來出售由預期價格(即上一期價格)所決定的產量。這種實際價格和預期的價格不吻合,造成了產量和價格的波動。但是,這種解釋是不全面的。因為生產者從自己的經驗中,會逐步修正自己的預期價格,使預期價格接近實際價格,從而使實際產量接近市場的實際需求量。
事例
關於這一點,西方經濟學家阿西瑪普羅斯舉出了以下的事例:
在美國,1972年由於暴風雨的惡劣氣候,土豆產量大幅度下降,從而土豆價格上漲.隨著土豆價格的上漲,農場主便擴大土豆的種植面積,使土豆產量在1974年達到歷史最高水平。結果,土豆供給量大幅度增加導致土豆價格又急劇下降,以緬因州土豆為例,0.4536千克土豆的價格由1974年5月的13美分降為1975年3月的2美分,該價格比平均生產成本還低。這種現象可以用蛛網模型來解釋。作為補充,阿西瑪又舉了一個特殊的例子來說明蛛網模型的缺陷:在普林斯愛德華島嶼,當農場主們都因土豆價格下降而縮減土豆的種植面積時,惟有一個農場主不是這樣做。因為這個農場主根據長期的經營經驗,相信土豆價格將上升,而眼下正是自己增加土豆生產的時候。可見,這個農場主的預期和行為與蛛網模型所分析的情況是不吻合的。