簡述
定積分的積分區間都是有限的,被積函式都是有界的。但在實際套用和理論研究中,還會遇到一些在無限區間上定義的函式或有限區間上的無界函式,對它們也需要考慮類似於定積分的問題。因此,有必要對定積分的概念加以推廣,使之能適用於上述兩類函式。這種推廣的積分,由於它異於通常的定積分,故稱之為廣義積分,也稱之為反常積分。
幾何意義
反常積分存在時的幾何意義:函式與X軸所圍面積存在有限制時,即便函式在一點的值無窮,但面積可求。
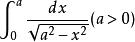 反常積分
反常積分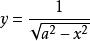 反常積分
反常積分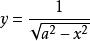 反常積分
反常積分例如的幾何意義是:位於曲線之下,X軸之上,直線x=0和x=a之間的圖形面積,而x=a點的值雖使無窮,但面積可求。
類型
1.無窮區間反常積分
每個被積函式只能有一個無窮限,若上下限均為無窮限,則分區間積分。
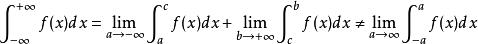 反常積分
反常積分2.無界函式反常積分
即瑕積分,每個被積函式只能有一個瑕點,多個瑕點則分區間積分。
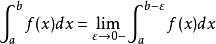 反常積分
反常積分(f(b)無界)
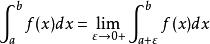 反常積分
反常積分(f(a)無界)
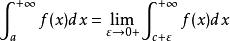 反常積分
反常積分(區間內點f(c)無界)
3.混合反常積分
對於上下限均為無窮,或被積分函式存在多個瑕點,或上述兩類的混合,稱為混合反常積分。對混合型反常積分,必須拆分多個積分區間,使原積分為無窮區間和無界函式兩類單獨的反常積分之和。
斂散性判斷
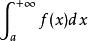 反常積分
反常積分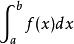 反常積分
反常積分反常積分的斂散判斷本質上是極限的存在性與無窮小或無窮大的比階問題。首先要記住兩類反常積分的收斂尺度:對第一類無窮限而言,當x→+∞時,f(x)必為無窮小,並且無窮小的階次不能低於某一尺度,才能保證收斂;對第二類無界函式而言,當x→a+時,f(x)必為無窮大。且無窮小的階次不能高於某一尺度,才能保證收斂;這個尺度值一般等於1,注意識別反常積分。

