平行線的判定
平行線
 平行線的判定
平行線的判定在同一平面內,永不相交的兩條直線叫平行線(parallel lines)。
特性
不平行兩條直線一定相交,平行用符號“∥”表示。,在同一平面內,經過直線外一點,與直線平行的直線只有一條。
平行公理
在歐幾里得的幾何原本中,第五公設(又稱為平行公理)是關於平行線的性質。它的陳述是:
“如果兩條直線被第三條直線所截,一側的同旁內角之和大於兩個直角,那么最初的兩條直線相交於這對同旁內角的另一側。”
這條公理的陳述過於冗長。在1795年,蘇格蘭數學家Playfair提出了以下以下公理作為平行公理的代替,在被人們廣泛的使用。
在同一平面內,過直線外一點,有且只有一條直線與這條直線互相平行。
平行公理的推論:(平行線的傳遞性) 如果兩條直線都和第三條直線平行,那么這兩條直線也互相平行。可以簡稱為:平行於同一條直線的兩條直線互相平行。
判定方法
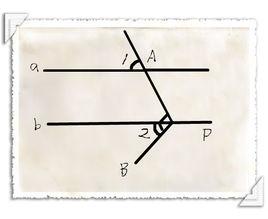
在同一平面內,兩條直線被第三條直線所截,如果同位角相等,那么這兩條直線平行。也可以簡單的說成:
1.同位角相等兩直線平行
在同一平面內,兩條直線被第三條直線所截,如果內錯角相等,那么這兩條直線平行。也可以簡單的說成:
2.內錯角相等兩直線平行
在同一平面內,兩條直線被第三條直線所截,如果同旁內角互補,那么這兩條直線平行。也可以簡單的說成:
3.同旁內角互補兩直線平行。
簡單的判定方法
同位角相等,兩直線平行。
內錯角相等,兩直線平行。
同旁內角互補,兩直線平行。
在同一平面內,兩直線不相交,即平行、重合。
兩條直線平行於一條直線,則三條不重合的直線互相平行。
(相反判定方法)
兩直線平行,同位角相等。
兩直線平行,內錯角相等。
兩直線平行,同旁內角互補。
如果兩條直線都與第三條直線平行,
那么這兩條直線也互相平行。
1.同位角相等,兩直線平行。
2.內錯角相等,兩直線平行。
3.同旁內角互補,兩直線平行。
4.在同一平面內,兩直線不相交,即平行、重合。
5.兩條直線平行於一條直線,則三條不重合的直線互相平行。
(
6.兩直線平行,同位角相等。
7.兩直線平行,內錯角相等。
8.兩直線平行,同旁內角互補。
如果兩條直線都與第三條直線平行,
那么這兩條直線也互相平行。
結果
同一平面內,垂直於同一條直線的兩條線段(直線)平行
(同一平面內),平行於同一條直線的兩條線段(直線)平行
同一平面內,永不相交的兩條直線叫平行線
過直線外一點有且僅有一條直線與已知直線平行
1.同一平面內,垂直於同一條直線的兩條線段(直線)平行
2.(同一平面內),平行於同一條直線的兩條線段(直線)平行
3.同一平面內,永不相交的兩條直線叫平行線
4.過直線外一點有且僅有一條直線與已知直線平行