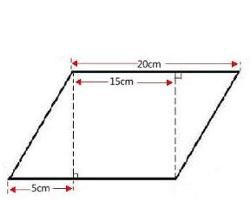
性質
平行四邊形的性質：
（1）：平行四邊形對邊分別相等；
（2）：平行四邊形對邊分別平行；
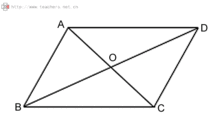平行四邊形的判定（3）：平行四邊形對角分別相等；
（4）：平行四邊形對角線互相平分；
（5）：平行四邊形鄰角互補
符號表示為
∵四邊形ABCD是平行四邊形
∴AB∥CD AD∥BC
AB=CD AD=BC
∠A=∠C ∠B=∠D
（此中未體現對角線平分與鄰角互補）
判定方法
平行四邊形的判定方法
平行四邊形的判定1.兩組對邊分別平行的四邊形是平行四邊形（定義判定法）；
2.一組對邊平行且相等的四邊形是平行四邊形；
3.對角線互相平分的四邊形是平行四邊形；
4.兩組對角分別相等的四邊形是平行四邊形；（例題3）
5.所有鄰角（每一組鄰角）都互補的四邊形是平行四邊形；
6.兩組對邊分別相等的四邊形是平行四邊形。
輔助線
一、連線對角線或平移對角線。
二、過頂點作對邊的垂線構成直角三角形。
三、連線對角線交點與一邊中點，或過對角線交點作一邊的平行線，構成線段平行或中位線。
四、連線頂點與對邊上一點的線段或延長這條線段，構造相似三角形或等積三角形。
五、過頂點作對角線的垂線，構成線段平行或三角形全等。
面積、周長
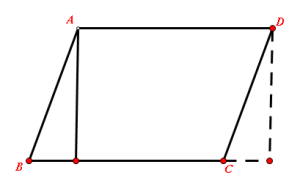平行四邊形（2）平行四邊形的面積等於兩組鄰邊的積乘以夾角的正弦值；如用“a”“b”表示兩組鄰邊長，α表示兩邊的夾角，“S”表示平行四邊形的面積，則S平行四邊形=ab*sinα。
2、平行四邊形周長：四邊之和。可以二乘（底1+底2）；如用“a”表示底1，“b”表示底2，“c平”表示平行四邊形周長，則平行四邊的周長c=2(a+b)。
類別
1、平行四邊形屬於平面圖形。
2、平行四邊形屬於四邊形。
3、平行四邊形中還包括特殊的平行四邊形：矩形，正方形和菱形等。
4、平行四邊形屬於中心對稱圖形。
例題
例1
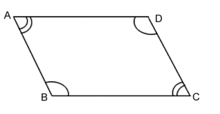
平行四邊形的判定已知，在四邊形ABCD中， ∠A=∠C，AB∥CD。求證：四邊形ABCD是平行四邊形。
證明：∵∠A=∠C，AB∥CD
∴∠B=∠D(等角的補角相等）
∵∠A=∠C且∠B=∠D
∴四邊形ABCD是平行四邊形（兩組對角分別相等的四邊形是平行四邊形）
例2
已知平行四邊形ABCD中，對角線AC和BD相交於點O，AC=10，BD=8．
（1）若AO⊥BD，試求四邊形ABCD的面積；
（2）若AC與BD的夾角∠AOD=60° ，求四邊形ABCD的面積；
（3）試討論：若把題目中“平行四邊形ABCD”改為“四邊形ABCD”，且∠AOD=θ
AC=a ，BD=b ，試求四邊形ABCD的面積（用含θ，a，b的代數式表示）．
平行四邊形的判定解：（1）∵AC⊥BD
∴四邊形ABCD的面積S=1/2AC×BD
=1/2×10×8
=40
（2）過點A分別作AE⊥BD，垂足為E
∵四邊形AB CD為平行四邊形AO=CO=1/2AC=5，
BO=DO=1/2BD=4
在Rt⊿AOE中， sin∠AOE=AB/AO
∴ AE=AO×sin ∠AOE=AO×sin60°=5×√3/2=5√3/2
∴S△AOD=1/2OD×AE=1/2×4×√3/2×5=5√3
∴四邊形ABCD的面積S=4S△AOD=20√3
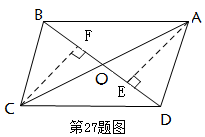第3問圖(3）如圖所示過點A,C分別作AE⊥BD，CF⊥BD，垂足分別為E,F在Rt⊿AOE中，sin∠AOE=AE/AO
∴ AE=AO×sin∠AOE=AO×sinq
同理可得 CF=CO×sin∠COF=CO×sinq
∴四邊形ABCD的面積S=S△ABD+S△CBD=1/2BD×AE+1/2BD×CF
=1/2BD×sinq（AO+CO）
=1/2BD×ACsinq
=1/2absinq
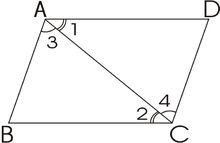
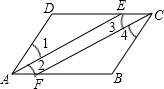
〔3〕如圖所示，在平行四邊形ABCD中，AE、CF分別是∠DAB、∠BCD的平分線，求證：四邊形AFCE是平行四邊形．
分析：由四邊形ABCD是平行四邊形，可得，CE∥AF，∠DAB=∠DCB，又AE、CF分別平分∠DAB、∠BCD，所以∠2=∠3，可證四邊形AFCE是平行四邊形．
解答：
證明：∵四邊形ABCD是平行四邊形，
平行四邊形的判定∴CE∥AF，∠DAB=∠DCB，
∵AE、CF分別平分∠DAB、∠BCD，∴∠2=∠3，
又∠3=∠CFB，
∴∠2=∠CFB，
∴AE∥CF，
又CE∥AF，
∴四邊形AFCE是平行四邊形．
例3
平行四邊形的判定在四邊形ABCD中，已知∠A=∠C，∠B=∠D,求證四邊形ABCD為平行四邊形。
證明：∵∠A=∠C，∠B=∠D，∠A+∠C+∠B+∠D=360°
∴2（∠A+∠B）=360°
∴∠A+∠B=180°
即AD∥BC
同理，可得AB∥CD
∴四邊形ABCD為平行四邊形
過平行四邊形對角線的交點任一直線平分平行四邊形的面積。
例4
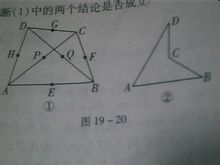
已知任意四邊形ABCD，且線段AB，BC,CD,DA,AC,BD的中點分別是E,F,G,H,P,Q（1）若四邊形ABCD如圖①，判斷一些結論是否正確（要寫出為什麼） 甲：順次連線E,F,G,H一定得到平行四邊形。 乙;順次連線E,Q,G,P一定得到平行四邊形。（2）若四邊形ABCD如圖②，請你判斷（1）中的兩個結論是否成立（也要寫出理由，有過程）
平行四邊形的判定答 (1)甲：一定會得到平行四邊形因為E,F,G,H分別為AB,BC,CD，DA中點所以EF=0.5AC=GH GF=0.5BD=EH(且平行，因為三角形兩條邊的中點的連線平行且等於另外一條邊的一半。）所以EF平行且等於GH GF平行且等於EH所以連線EFGH會得到一個平行四邊形。
乙：因為E,Q,G,P分別為AB,BD,CD，CA中點所以EQ平行且等於0.5AD平行且等於GP GQ平行且等於0.5BC平行且等於EP所以EQ平行且等於GP GQ平行且等於EP所以連線EQGP會得到一個平行四邊形。
(2)是同樣的理論，將圖畫出來，帶進去看就知道了
