概念
數學中,術語“ 平凡”(“ 平凡的”)經常用於結構非常簡單的對象(比如群或拓撲空間),有時亦會用明顯或乏趣這兩個詞代替,但對非數學工作者來說,它們有時可能比其他更複雜的對象更難想像或理解。
例如:
•明顯因數:對於每個正整數 n 來說,1、-1、n 和 -n 都是它的明顯因數。
•空集:不包含任何元素的集合;
•平凡群:只含單位元的群;
•平凡環:定義於單元素集合的環。
定義
一般,Ax=0中的零解,即x=0,稱為 平凡解。
矩陣代數的中的定義,AX=0, 行列式|A|≠0, 則X只有平凡解X=0,無非平凡解.
因為任何線性空間的子空間都過零點,所以明顯的等於0的時候解是成立的,但這顯然沒什麼意義,說這個0解是平凡的。
通俗來講,如果方程組AX=0, 只有當X=0的時候才成立,就說方程組AX=0隻有平凡解(trivial solution),此時肯定有行列式|A| 不為零。相反如果方程組AX=0存在非零解,也就是說存在不為零的X也可以使方程組AX=0成立,則說方程組AX=0存在非平凡解(nontrivial solution),此時肯定有係數矩陣行列式的值|A|=0 。
 平凡解
平凡解例如,考慮微分方程:。
這裡 y= f( x) 為函式,其導數為 y′。
y= 0,0 函式是平凡解;
y(x) = e,指數函式是一個非平凡解。
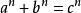 平凡解
平凡解 平凡解
平凡解類似地,數學家經常將費馬大定理描述為方程對 n> 2 沒有非平凡解。 顯然,這個方程確實有解。比如對任何 n都是解, a= 1, b= 0, c= 1 也一樣。但是這種解是顯然而無趣的,從而稱為 平凡解。
擴展
數學推理
平凡也經常指證明中容易的情形,為了完整性而不能省略。比如,數學歸納法證明分為兩部分:“奠基步驟”是對一個特殊起始值比如 n= 0 或 n= 1 證明定理;然後歸納步驟證明如果定理對特定值 n成立,那么對 n+1 也成立。奠基情形經常是顯然的。(但是,也有歸納步驟是平凡的而奠基情形卻困難的例子。關於多項式的定理經常是這種類型,證明對變元的個數用歸納法。證明如果係數環 A是唯一分解整環那么 A[ X,..., X] 是唯一分解整環,歸納步驟只要簡單的寫成 A[ X,..., X] = A[ X,..., X][ X],而一個變元的奠基情形是困難的。)類似地,我們可能想證明某種性質對一個集合中所有元素都成立。證明的主要考慮非空集合,詳細檢驗其元素是否具有該性質;但如果集合是空集,則性質對其所有元素都成立,因為沒有元素需要檢驗。
數學界一個常見的笑話是說“平凡”和“被證明了的”是同義詞——這就是說,任何定理如果已知成立就可以認為是“平凡”的。另一個笑話是關於兩個數學家討論一個定理。第一個數學家說某個定理是“平凡的”。另一個要求一個解釋,然後他進行了 20 分鐘的解說。解說完了之後,第二個數學家同意這個定理是平凡的。這個笑話指出對平凡性判斷的主觀性。舉個例子,對微積分熟練的人,會認為這個定理
 平凡解
平凡解是平凡的。但對初學者來說,可能一點也不顯然。
值得注意的是,平凡性也取決於語境。泛函分析中的證明可能會給出一個數,平凡地假設存在這樣的大數。在初等數論中證明自然數的基本結論時,證明也許會與“每個自然數都有一個後繼”息息相關,但此點需加以證明,或者將其作為一個公理。
相關知識
非平凡解
