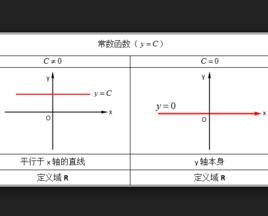
定義
在數學中, 常數函式(也稱 常值函式)是指值不發生改變(即是常數)的函式。例如,我們有函式 f(x)=4,因為 f映射任意的值到4,因此 f是一個常數。更一般地,對一個函式 f: A→B,如果對 A內所有的 x和 y,都有 f(x)=f(y),那么, f是一個常數函式。
請注意,每一個空函式(定義域為空集的函式)無意義地滿足上述定義,因為 A中沒有 x和 y使 f(x)和 f(y)不同。然而有些人認為,如果包括空函式的話,那么常數函式將更容易定義。
對於多項式函式,一個非零常數函式稱為一個零次多項式。
性質
常數函式可以通過與複合函式的關係,從兩個途徑進行描述。
下面這些是等價的:
f: A→B是一個常數函式。 對所有函式 g, h: C→A, fog=foh(“o”表示複合函式)。 f與其他任何函式的複合仍是一個常數函式。 上面所給的常數函式的第一個描述,是範疇論中常數態射更多一般概念的激發和定義的性質。
根據定義,一個函式的導函式度量自變數的變化與函式變化的關係。那么我們可以得到,由於常數函式的值是不變的,它的導函式是零。
例如:
如果 f是一個定義在某一區間、變數為實數的實數函式,那么若且唯若 f的導函式恆為零時, f是常數。 對預序集合間的函式,常數函式是保序和倒序的;相反的,如果 f既是保序的也是倒序的,如 f的定義域是一個格,那么 f一定是一個常數函式。
常數函式的其他性質包括:
任一定義域和陪域相同的常數函式是等冪的。 任一拓撲空間上的常數是連續的。 在一個連通集合中,若且唯若 f是常數時,它是局部常數。
相關函式
在數學領域,兩個函式的 複合函式指一個將第一個函式作用於參數,然後再將第二個函式作用於所得結果的函式。
具體來說,給定兩個函式 f: X→ Y和 g: Y→ Z,其中 f的陪域等於 g的定義域(稱為 f、 g 可複合),則其複合函式,記為 g∘ f,以 X為定義域, Z為陪域,並將任意 x∈ X映射為 g( f( x))。有時也省略複合記號“∘”,直接寫作 g f。
g∘ f中的“∘”稱作ring運運算元。
函式的複合滿足結合律:若 f、 g可複合, g、 h可複合,則有:
•h∘ (g∘f)=(h∘g) ∘f
函式的複合可以看作是二元關係複合的一個特例。