概念
對於求 分式型的函式,常採用拆項使分式的分子為常數,有些分式函式可以拆項分成一個整式和一個分式(該分式的分子為常數)的形式,這種方法叫 分離常數法。分離常數法常用於求函式最值或值域等,在數列求和中也常用到,可參考例題理解。
還有一種分離常數法的套用方式是在含有兩個量(一個常量和一個變數)的關係式(不等式或方程)中,要求變數的取值範圍,可以將變數和常量分離(即變數和常量各在式子的一端),可參考“適用條件”中舉的例子和例題6。
適用情況舉例
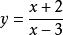 分離常數法
分離常數法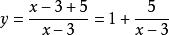 分離常數法
分離常數法(1)分離常數法適用於解析式為分式形式的函式,如求的值域,則可分離常數為,進而求值域, 當分式的分子和分母次數相同時,常可分離出一個常數來,稱之分離常數法。
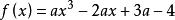 分離常數法
分離常數法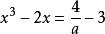 分離常數法
分離常數法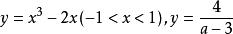 分離常數法
分離常數法(2) 在含有兩個量(一個常量和一個變數)的關係式(不等式或方程)中,要求變數的取值範圍,可以將變數和常量分離(即變數和常量各在式子的一端),從而求出變數的取值範圍,如:已知函式在區間(-1,1)上有唯一的零點,求a的取值範圍。可轉化為“關於x的方程在(-1,1)上有唯一的零點”,即“函式的圖像有唯一公共點”。這道題就有一個常量a,一個變數x,這裡就將常量a分離出來進而可以求。可參考例題6。
分式型情況
求分式函式的值域
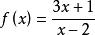 分離常數法
分離常數法例1 設x小於等於1 ,求函式的值域。
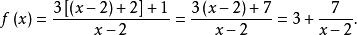 分離常數法
分離常數法解: 由已知有
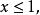 分離常數法
分離常數法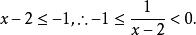 分離常數法
分離常數法由得
 分離常數法
分離常數法 分離常數法
分離常數法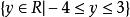 分離常數法
分離常數法函式的值域為,
求分式函式的最值
 分離常數法
分離常數法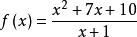 分離常數法
分離常數法例2 設求函式的最小值。
 分離常數法
分離常數法解:
由已知有
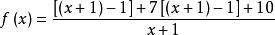 分離常數法
分離常數法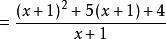 分離常數法
分離常數法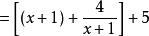 分離常數法
分離常數法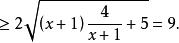 分離常數法
分離常數法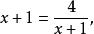 分離常數法
分離常數法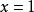 分離常數法
分離常數法 分離常數法
分離常數法若且唯若即時,等式成立,所以當x=1時,取得最小值9。
在函式奇偶性中的套用
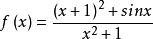 分離常數法
分離常數法例3 設函式的最大值為M,最小值為m,則M+m為多少?
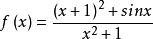 分離常數法
分離常數法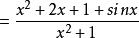 分離常數法
分離常數法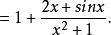 分離常數法
分離常數法解:
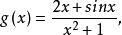 分離常數法
分離常數法 分離常數法
分離常數法 分離常數法
分離常數法令易得為奇函式,其圖像關於原點對稱,所以最大值與最小值之和為零,所以M+m=2。
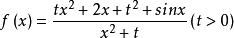 分離常數法
分離常數法變式:若關於x的函式的最大值為M,最小值為N,且M+N=4,則實數t的值為多少?(答案為2)
評註: 題目中出現最大值與最小值之和等問題,可轉化為對稱性問題解決,通過分離常數後出向奇函式,結合圖像的對稱性可以迅速解題。
用於函式圖像的作圖
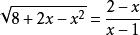 分離常數法
分離常數法例4 方程的實根共有幾個?
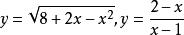 分離常數法
分離常數法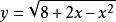 分離常數法
分離常數法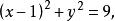 分離常數法
分離常數法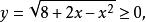 分離常數法
分離常數法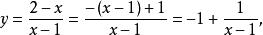 分離常數法
分離常數法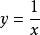 分離常數法
分離常數法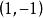 分離常數法
分離常數法解: 本題可轉化為求圖像交點個數。將平方整理得由於所欲圖像為x軸上方的一個半圓。又所以圖像是由圖像向右、向下平移一個單位後得到的,其對稱中心為,易得兩圖像交點個數為1。
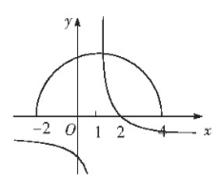 圖1
圖1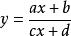 分離常數法
分離常數法評註:形如函式都可以通過分離常數進行處理,將之轉化為反比例函式,再通過平移或變換得到。有了圖像就可以使很多數形結合的問題容易得到解決。
在數列中的套用
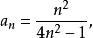 分離常數法
分離常數法 分離常數法
分離常數法例5 設求數列的前n項和S
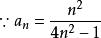 分離常數法
分離常數法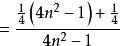 分離常數法
分離常數法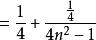 分離常數法
分離常數法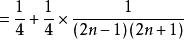 分離常數法
分離常數法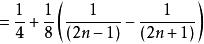 分離常數法
分離常數法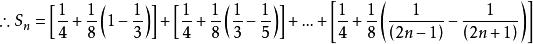 分離常數法
分離常數法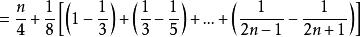 分離常數法
分離常數法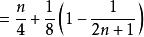 分離常數法
分離常數法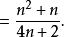 分離常數法
分離常數法評註: 通過對an分離常數後,出現典型的裂項求和。
常量與變數分離情況
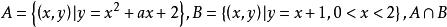 分離常數法
分離常數法例6 設集合是單元素集,求實數a的取值範圍。
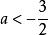 分離常數法
分離常數法這是某資料上的一道例題,給出的答案是.此答案也是錯誤的.若用分離常’數法求解就不易出錯。
 分離常數法
分離常數法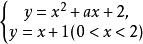 分離常數法
分離常數法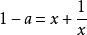 分離常數法
分離常數法 分離常數法
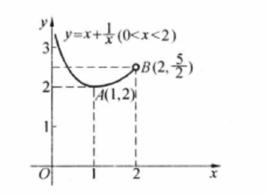
分離常數法解: 題意即關於的方程組有唯一一組解,也即關於x的方程在(0,2)上有唯一解,得關於的方程組
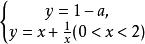 分離常數法
分離常數法有唯一解。
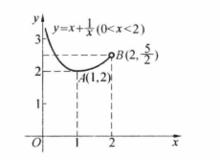 圖2
圖2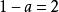 分離常數法
分離常數法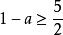 分離常數法
分離常數法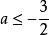 分離常數法
分離常數法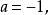 分離常數法
分離常數法由圖2得,或,即或這就是所求a的取值範圍。