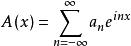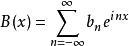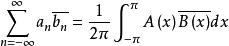帕塞瓦爾定理

在數學中，帕塞瓦爾定理經常指“傅立葉轉換是么正算符”這一結論；簡而言之，就是說函式平方的和（或積分）等於其傅立葉轉換式平方之和（或者積分）。這個定理產生於Marc-Antoine Parseval在1799年所得到的一個有關級數的定理，該定理隨後被套用於傅立葉級數。它也被稱為瑞利能量定理或瑞利恆等式，以物理學家約翰·斯特拉特，第三代瑞利男爵命名。 雖說這一術語常用來描述傅立葉轉換的么正性，尤其是在物理學和工程學上，但這種屬性最一般的形式還是稱為Plancherel theorem而不是才更合適。

定理含義

一個信號所含有的能量（功率）恆等於此信號在完備正交函式集中各分量能量（功率）之和。

定理形式

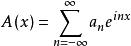帕塞瓦爾定理

假定 A( x)和 B( x)都是平方可積的（參照勒貝格測度）複變函數，且定義在 R上周期為2π的區間上，分別寫成傅立葉級數的形式：

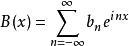帕塞瓦爾定理

則有：

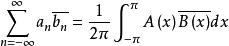帕塞瓦爾定理