定義及延伸
在數學裡的泛函分析中， 貝塞爾不等式是類似於勾股定理的一種不等式。貝塞爾不等式揭示了希爾伯特空間中的一個元素和它在一個正交序列上的投影之間的關係。
舉例來說，平面上的一個向量的長度的平方等於它在兩個相互垂直的坐標軸上的投影的平方和，而對於一個三維空間上的向量，它在兩個相互垂直的坐標軸上的投影的平方和一般會小於它自身的長度的平方，除非它就在這兩個坐標軸構成的平面上。對於一個希爾伯特空間中的向量來說，它在任意一個正交序列上的投影的平方和也是小於等於它自身的長度的平方。這就是貝塞爾不等式。貝塞爾不等式的等號成立若且唯若正交序列是完全序列。這時貝塞爾不等式轉化為 帕塞瓦爾定理。
貝塞爾不等式
貝塞爾不等式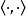
貝塞爾不等式 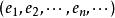貝塞爾不等式設 是一個裝備了內積： 的希爾伯特空間。考慮一組規範正交向量的序列： 。那么，對於任意一個 中的元素，都有：
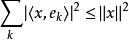貝塞爾不等式
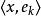貝塞爾不等式
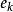貝塞爾不等式其中的係數 是 x在一個正交向量序列中元素 上的投影的長度。
例子
例一
平面直角坐標系
貝塞爾不等式
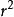貝塞爾不等式
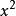貝塞爾不等式
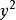貝塞爾不等式平面上的向量滿足勾股定理。在平面上，假定已經存在一個由相互垂直的向量構成的直角坐標系。根據勾股定理，一個向量的長度的平方 等於它在 X軸的投影的長度的平方( )加上它在 Y軸的投影的長度的平方( )，如圖。
實際上，整個平面上的每一個向量都可以由這兩個相互垂直的單位向量的有限線性組合表示。這樣的一組相互垂直的向量被稱為是這個平面里的一組 完全規範。
正交向量：每個向量都可以被這一組向量的有限線性組合作任意程度的逼近（事實上是等於）。
例二
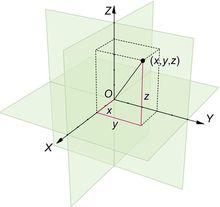
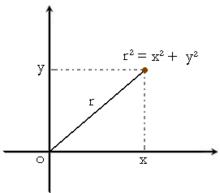
貝塞爾不等式三維空間中的平面投影
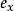貝塞爾不等式
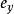貝塞爾不等式當向量是在三維歐幾里得空間中時，對於一個平面（比如說xOy平面）以及平面上的一個由相互垂直的向量（Ox 方向上的 和Oy 方向上的 ）構成的直角坐標系，向量的長度的平方會比它在 X軸的投影的長度平方加上它在 Y軸的投影的長度平方之和還要大。實際上，這個平方和正是向量在xOy平面上的投影的長度的平方。而原來的向量的長度的平方是這個投影長度的平方加上它在 Z軸的投影的長度平方。
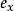貝塞爾不等式 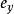貝塞爾不等式這個事實說明，向量 和 不是三維歐幾里得空間裡的一組完全正交向量。
證明
證明的思路是利用一般希爾伯特空間中的“勾股定理”：如果兩個向量垂直，那么它們的和的長度平方等於它們兩個的長度的平方和。首先考慮規範正交向量序列有限時的情形：設序列的長度是 n，序列中的元素是：
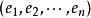貝塞爾不等式
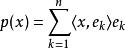貝塞爾不等式
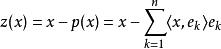貝塞爾不等式設一個向量 x在這個規範正交序列上的投影為向量： ，而 x與它的投影的差則是向量： 。這兩個向量的內積等於：
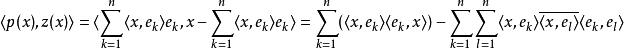貝塞爾不等式
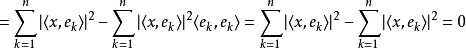貝塞爾不等式也就是說， x在這個規範正交序列上的投影垂直於 x與它的投影的差。所以根據勾股定理，有：
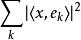貝塞爾不等式
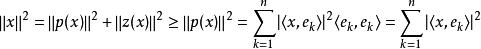貝塞爾不等式
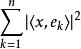貝塞爾不等式
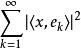貝塞爾不等式
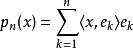貝塞爾不等式 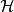貝塞爾不等式即使規範正交向量序列是無限的，只要它是可數的，就會有相同的不等式。實際上，只需要考慮這個無窮（可數個）序列中的前面 n項。根據有限序列時的情形，可以證明一個元素 x在規範正交向量序列的前 n項上的投影的長度平方和 小於等於 x的長度平方。這個平方和實際上是正項無窮級數的前 n項部分和，所以這個無窮級數收斂，並且其極限 也小於等於 x的長度平方。換句話說，向量序列 在 上收斂。
