概念
1、在一平面上取任一閉合區域,其面積為S,使它沿垂直於該區域的平面運動形成一個體積為V的立體,那么這個立體圖形的體積就等於質心所經路程r乘以區域面積。表達式為V=S·r。
2、如果令某一長為L的曲線段,其長度為L,使它沿著垂直於它所在平面的方向掃過一個面積S,那么這個面積的大小就等於線段的質心移動的距離r乘以線段的長度。表達式為S=L·r。
注意:是質心,而不是重心,求半圓面質心,因為除非重力場是均勻的,否則同一物質(系統)的質心與重心通常不在同一假想點上。
套用
套用一
 巴普斯定理
巴普斯定理巴普斯定理用來求平面圖形的質心是十分方便的,例如下面這個例子:
求半圓面質心。
令半圓面繞著它的直徑旋轉形成一個球體,假設半圓面的半徑為R,那么它的面積即為S=πR^2/2,所得球體體積為V=4πR^3/3,又設質心離半圓面的圓心距離為X,則質心旋轉一周經過的路程為L=2πX,由巴普斯定理得V=SL,所以X=4R/3π.
類似地,我們也可以求得三角形或其他平面幾何圖形的質心。
套用二
當然,巴普斯定理既然可以利用平面圖形旋轉後的體積來求質心,那么它也可以利用質心位置來求旋轉體的體積。例:
求圓錐體體積:
圓錐是由一個直角三角形繞直角邊旋轉得來的,所以它的體積等於三角形的質心到直角邊的距離乘以直角三角形的面積,而三角形質心到直角邊的距離又是直角邊上高的1/3,於是體積的計算就十分簡單了。
類似地,我們也可以求得圓環體等的體積。
定理2的套用
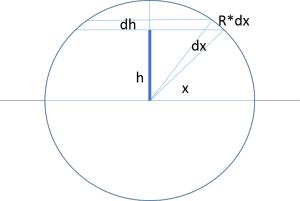
1、圓面積公式的又一證法:
將長為R的線段OP繞過O點且垂直於該線段的軸旋轉一周即得到半徑為R的圓O,質心經過路程為2π*(1/2)R=πR,所以S=πR*R=πR^2。
2、圓環體表面積
圓心O距中心軸M的長度為R,圓O半徑為r,則圓O周長為2πr,將它沿垂直於其所在平面的方向繞M軸一周后質心O移動路程2πR,所以旋轉得到的空心圓環體的表面積為2πr*2πR=4π^2Rr。