簡介
尺規作圖就是只使用直尺和圓規,並且只準許使用有限次,來解決不同的平面幾何作圖題。
這裡的“直尺”和“圓規” 跟現實中的並非完全相同,具有抽象意義。
直尺必須沒有刻度,無限長,且只能使用直尺的固定一側。只可以用它來將兩個點連在一起,不可以在上畫刻度。圓規可以開至無限寬,但上面亦不能有刻度。它只可以拉開成你之前構造過的長度或一個任意的長度。
同時,僅以“有限次使用無刻度的直尺和圓規作圖”這樣的措辭作為定義顯然是不夠嚴密的,因為不限定每“次”以內的操作複雜度的話,“有限次”就成無意義的了。
因此,一般採用的定義是基於“作圖公法”的定義,即:
1. 每次的操作只能是公認允許的五項基本操作(稱為五項作圖公法)之一。
2. 每次操作之前,操作者為決定是否操作和進行哪種操作可以進行的邏輯判斷,也只能是幾何學中公認允許的幾種。
基於“作圖公法”的定義如下:
尺規作圖定義
承認以下五項前提,有限次運用以下五項公法而完成的作圖方法,就是合法的尺規作圖:
五項前提是:
(1) 允許在平面上、直線上、圓弧線上已確定的範圍內任意選定一點(所謂“確定範圍”,依下面四條的規則)。
(2) 可以判斷同一直線上不同點的位置次序。
(3) 可以判斷同一圓弧線上不同點的位置次序。
(4) 可以判斷平面上一點在直線的哪一側。
(5) 可以判斷平面上一點在圓的內部還是外部。
五項公法是:
(1) 根據兩個已經確定的點作出經過這兩個點的直線。
(2) 以一個已經確定的點為圓心,以兩個已經確定的點之間的距離為半徑作圓。
(3) 確定兩個已經做出的相交直線的交點。
(4) 確定已經做出的相交的圓和直線的交點。
(5) 確定已經做出的相交的兩個圓的交點。
也有些資料上給出的五項公法的後兩條中的“交點”改為“公共點”。這兩種敘述差別在於後者多包括了“切點”。但是,因為確定切點即使不算基本操作,也是可以用其它基本操作組合實現的。所以,兩種敘述的定義並無本質不同。
歷史
古希臘
尺規作圖,起源於古希臘。
希臘人強調作圖只能用直尺圓規,有下列原因:
①希臘幾何的基本精神,是從極少的基本假定(定義、公理、公設)出發,推導出儘可能多的命題。
②受柏拉圖哲學思想的影響。
③以畢達哥拉斯學派為代表的希臘人認為圓是最完美的平面圖形,圓和直線是幾何學最基本的研究對象。
史上最早明確提出尺規限制的是伊諾皮迪斯,他發現以下作圖法:在已知直線的已知點上作一角與已知角相等。伊諾皮迪斯以後,尺規的限制逐漸成為一種公約,最後總結在《幾何原本》之中。
中國古代
“規”就是圓規,是用來畫圓的工具,在我國古代甲骨文中就有“規”這個字。“矩”就像木工使用的角尺,由長短兩尺相交成直角而成,兩者間用木槓連線以使其牢固,其中短尺叫勾,長尺叫股。
矩的使用是我國古代的一個發明,山東歷城武梁祠石室造像中就有“伏羲氏手執矩,女媧氏手執規”之圖形.矩不僅可以畫直線、直角,加上刻度可以測量,還可以代替圓規.甲骨文中也有矩字,這可追溯到大禹治水(公元前2000年)前.
《史記》卷二記載大禹治水時“左準繩,右規矩”.趙爽注《周髀算經》中有“禹治洪水,……望山川之形,定高下之勢,……乃勾股之所由生也.”意即禹治洪水,要先測量地勢的高低,就必定要用勾股的道理.這也說明矩起源於很遠的中國古代.
春秋時代也有不少著作涉及規矩的論述,《墨子》卷七中說“輪匠(製造車子的工匠)執其規矩,以度天下之方圓.”《孟子》卷四中說“離婁(傳說中目力非常強的人)之明,公輸子(即魯班,傳說木匠的祖師)之巧,不以規矩,不能成方圓.”可見,在春秋戰國時期,規矩已被廣泛地用於作圖、製作器具了.由於我國古代的矩上已有刻度,因此使用範圍較廣,具有較大的實用性。
近代西方
由於對尺規作圖的限制,使得一些貌似簡單的幾何作圖問題無法解決.最著名的是被稱為幾何三大問題的三個古希臘古典作圖難題:立方倍積問題、三等分任意角問題和化圓為方問題.當時很多有名的希臘數學家,都曾著力於研究這三大問題,雖然藉助於其他工具或曲線,這三大難題都可以解決,但由於尺規作圖的限制,卻一直未能如願以償.以後兩千年來,無數數學家為之絞盡腦汁,都以失敗而告終.直到1637年笛卡爾創立了解析幾何,關於尺規作圖的可能性問題才有了準則。到了1837年萬芝爾首先證明立方倍積問題和三等分任意角問題都屬於尺規作圖不可能問題。1882年林德曼證明了π是超越數,化圓為方問題不可能用尺規作圖解決,這才結束了歷時兩千年的數學難題公案。
判定準則
從坐標系觀點看,所有的點和線都可以用坐標、方程的參量來代替,尺規作圖能夠完成兩根線段的和差積商,因此可做圖的數成為一個域。
直線和圓都是二次方程,稍微細緻的討論可知,尺規作圖能夠完成開平方,也就是域的二次擴張。
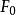 尺規作圖法
尺規作圖法 尺規作圖法
尺規作圖法因此,如果已知量與有理數生成的數域為,量可以尺規作圖的充要條件是,存在域塔:
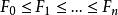 尺規作圖法
尺規作圖法其中相鄰的域擴張都是二次的。
換句話說,除了四則運算之外,只用到開平方的,可以尺規作圖。
但如果是開立方之類的情況,除了完全立方之類的特殊情況,一般不能尺規作圖。
當然,開四次方八次方,可以連續開平方,所以也是可以尺規作圖的。
策略
步驟
(1)解作圖題一般步驟:
①將題給的條件具體化;
②具體敘述所作圖形應滿足的條件;
③尋找作圖方法的途徑;
④根據分析所得的作圖方法作出正式圖形,並依次敘述作圖的過程;
⑤為了驗證所作的圖形是否正確,必須再根據已知的定義、公理、定理等,結合作法來證明所作的圖形完全滿足題中所要求的條件;
⑥研究這個問題是不是在什麼條件下都能作出圖形來.在什麼情況下,有唯一解,或多解,或沒有解。
(2)幾何作圖題的一般思路:
① 假設所求的圖形已經作出,並且滿足題中所有的條件。
② 分析圖中哪些是關鍵點,並探討確定關鍵點的方法。
③ 運用基本作圖法確定關鍵點,然後完成作圖。
常見的尺規作圖方法
(1)軌跡交點法
例如,電信部門要修建一座電視信號發射塔,按照設計要求,發射塔到兩個城鎮A、B的距離必須相等,到兩條高速公路m、n的距離也必須相等,發射塔應修建在什麼位置?
(2)代數作圖法:
例如,只用圓規,不許用直尺,四等分圓周(已知圓心)。
(3)旋轉作圖法:
例如,已知:直線a、b、c,且a∥b∥c。求作:正⊿ABC,使得A、B、C三點分別在直線a、b、c上。
(4)位似法作圖:
例如,已知:一銳角⊿ABC求作:一正方形DEFG,使得D、E在BC上,F在AC上,G在AB上。
(5)面積割補法
例如,過⊿ABC的底邊BC上一定點P,求作一直線l,使其平分⊿ABC的面積。
八種基本作圖
1、作一條線段等於已知線段
2、作一個角等於已知角
3、作已知線段的垂直平分線
尺規作圖
4、作已知角的角平分線
5、過一點作已知直線的垂線
6、已知一角、一邊作等腰三角形
7、已知兩角、一邊作三角形
8、已知一角、兩邊作三角形
作圖實例
過三點作圓
 尺規作圖法
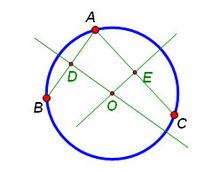
尺規作圖法【已知】不共線的A、B、C三點。
【求作】過該三點之圓。
【作法】① 連線AB,連線AC;② 分別作出線段AB、AC的中點D、E;③ 過D作AB的垂線,過E作AC的垂線,兩垂線相交於O;④ 以O為圓心OA長為半徑作圓,即為求作之圓。
作頂點分別在三平行線上的正三角形
 尺規作圖法
尺規作圖法【已知】平行直線L1、L2、L3。
【求作】正△ABC,使三個頂點分別落在三條平行線上。
【作法一】① L1上任取一點D為頂點,作正三角形△DBE,使B、E落在L2上(圖中虛線為正三角形簡易作法);② 作過D、E直線交L3於C;③ 以B為圓心BC為半徑作弧交L1於A,連線A、B、C成△ABC。
 尺規作圖法
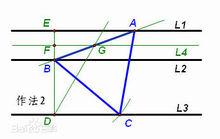
尺規作圖法【作法二】① L2上任取一點B作三平行線公垂線交L1於E,L3於D;② 作線段EB的垂直平分線L4;③ 過D作直線DG使∠EDG = 30°,並交L4於G;④過B、G作直線交L1於A;⑤ 以B為圓心BA為半徑作弧交L3於C,連線A、B、C成△ABC。
註:可將第⑤步改為,過G作AB的垂線交L3於點C.這樣G,B,D,C四點顯然共圓.於是可證得∠BCG=∠EDG = 30°.這樣可以很快證得△ABC為等邊三角形。
影響
幾何三大問題如果不限制作圖工具,便很容易解決。從歷史上看,好些數學結果是為解決三大問題而得出的副產品,特別是開創了對圓錐曲線的研究,發現了一批著名的曲線,等等。不僅如此,三大問題還和近代的方程論、群論等數學分支發生了關係。
