引理集

《引理集》 阿基米德著作之一 。當然這已不是歐幾里得幾何的尺規作圖法。

簡介

《引理集》 阿基米德著作之一
只有阿拉伯文譯本傳下來，是15個初等幾何的問題集．也許不是阿基米德的原著而是後人收集整理的，因為在文章中不止一次提到阿基米德的名字．

“皮匠刀”與三分角

其中提出一種被稱為“皮匠刀”(shoe-maker’s knife)的圖形，是三個半圓所包圍的部分，兩個小半圓外切，又同時內切於大半圓．這圖形有許多奇妙的性質，如通過兩小圓的外切點C，作CP⊥大圓直徑AB(三個圓的直徑是重合的)交大圓於P，則“皮匠刀”AGCBPA的面積等於以CP為直徑的圓面積．又可以作兩個小圓，分別切於CP、大圓及一個小圓，可證這兩個小圓相等．設HE是‖於AB的一個小圓的直徑，則切點F與H，A共線，F與E，B也共線．E是ΔABD的垂心，從A向DB作垂線，垂足I必落在大圓周上．又AE，HC必過切點G，等等。還有許多其他的性質．
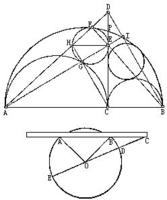
命題8和3等分角問題有關．設AB是⊙O的任一弦，延長AB至C使BC等於圓的半徑．聯CO並延長之使交圓於E，D．求證:
AE弧長=3倍的BD弧長。
聯OA，OB，只要證明∠AOE=3∠BOD即可．實際上 ∠AOE=∠OAC+∠OCA=∠OBA＋∠OCA=∠BOC＋2∠OCA=3∠BOD．
現將問題倒過來考慮．設有∠AOE，求它的三等分角．這就是古希臘的三大作圖問題之一的“三等分任意角”問題．從理論上說用直尺和圓規是不可能解決的．受到本命題的啟發，只要在直尺上加一個點，就能輕而易舉地解決這歷史難題．
在直尺ABC上記上一個點B，使B至尺端C的距離等於半徑．現令尺通過A點，B在圓周上移動，當C落在直徑的延長線EDC上時，作ABC直線，則∠C就是所求的三等分角．
當然這已不是歐幾里得幾何的尺規作圖法，因為工具已經改變(即使只加一點！)，而且不合作圖公法．不過它說明了一個問題，有些初學者只知道三等分角是難題，但不知難在尺規的限制上，如不限於尺規、那真是易如反掌．