定義
割圓曲線是在研究解古代三大作圖問題(化圓為方、三等分角和倍立方)時的一種數學成果.大約在公元前420年,希庇亞斯發現了割圓曲線,並發現它可以用於解三等分角和化圓為方兩個問題.
割圓曲線可由以下方法形成——
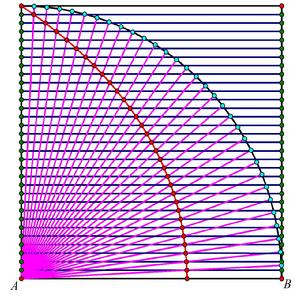
如圖,作一個正方形,它的底邊為AB.讓AB從底邊的位置開始沿逆時針方向,以一個固定的速度繞A點旋轉(紫).同時,AB也以一個同樣的速度運動(深藍).這兩條運動線段的交點所形成的便是割圓曲線(紅).
套用
三等分角若想三等分銳角或直角∠BAC,只需作一割圓曲線(如上圖),找出AC與割圓曲線的交點,再作CH垂直於AB,H在AB上。三等分CH,三等分點為D,使得DH=CH/3;再過點D作直線DE與AB平行,與割圓曲線交點為E。連線AE,則∠BAE=∠BAC/3。若是鈍角∠BAC,則可以先平分其為銳角,再三等分,然後再二倍即可。同理,亦可任意等分。
化圓為方若想作一正方形面積為一半徑為AM(M為割圓曲線於邊AB交點)的圓的面積,只需作一割圓曲線(如上圖),再作出一邊長為AM與2AB的矩形,則該矩形面積為半徑為AM的圓的面積。再求出AM與2AB的幾何平均數√(AM·2AB),則以此為邊的正方形的面積即為半徑為AM的圓的面積。
