公式
•利用三倍角公式
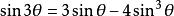三分之一角公式
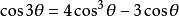三分之一角公式把它改為：
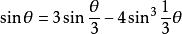三分之一角公式
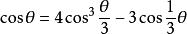三分之一角公式
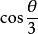三分之一角公式
三分之一角公式把 當成未知數， 當成常數項 ，解一元三次方程式即可求出：
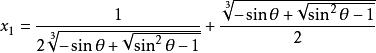三分之一角公式
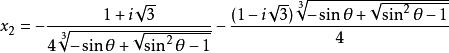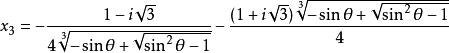三分之一角公式
三分之一角公式
三分之一角公式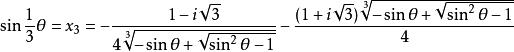
三分之一角公式當-90°≤ ≤90°時
三分之一角公式
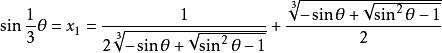三分之一角公式當90°≤≤450°時
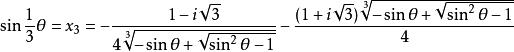三分之一角公式 三分之一角公式當450°≤≤630°時
三分之一角公式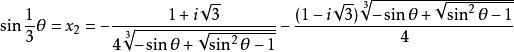
三分之一角公式當630°≤≤990°時
簡化
利用歐拉公式可以有效地簡化三分之一角公式
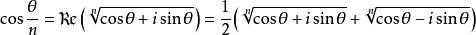三分之一角公式
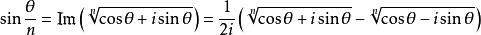三分之一角公式所以
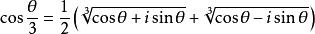三分之一角公式
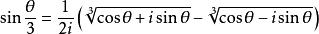三分之一角公式三等分角
三等分角是古希臘平面幾何里尺規作圖領域中的著名問題，與化圓為方及倍立方問題並列為尺規作圖三大難題。尺規作圖是古希臘人的數學研究課題之一，是對具體的直尺和圓規畫圖可能性的抽象化，研究是否能用規定的作圖法在有限步內達到給定的目標。三等分角問題的內容是：“能否僅用尺規作圖法將任意角度三等分？”
三等分角問題提出後，在漫長的兩千餘年中，曾有眾多的嘗試，但沒有人能夠給出嚴格的答案。隨著十九世紀群論和域論的發展，法國數學家皮埃爾·汪策爾首先利用伽羅瓦理論證明，這個問題的答案是否定的：不存在僅用尺規作圖法將任意角度三等分的通法。具體來說，汪策爾研究了給定單位長度後，能夠用尺規作圖法所能達到的長度值。所有能夠經由尺規作圖達到的長度值被稱為規矩數，而汪策爾證明了，如果能夠三等分任意角度，那么就能做出不屬於規矩數的長度，從而反證出通過尺規三等分任意角是不可能的。
如果不將手段局限在尺規作圖法中，放寬限制或藉助更多的工具的話，三等分任意角是可能的。然而，作為數學問題本身，由於三等分角問題表述簡單，而證明困難，並用到了高等的數學方法，在已證明三等分角問題不可能之後後，仍然有許多人嘗試給出肯定的證明。
