對稱差

數學上，兩個集合的對稱差是只屬於其中一個集合，而不屬於另一個集合的元素組成的集合。集合論中的這個運算相當於布爾邏輯中的異或運算。集合A和B的對稱差通常表示為AΔB，對稱差的符號在有些圖論書籍中也使用符號⊕來表示。例如：集合1，2，3和3，4的對稱差為1，2，4。所有學生的集合和所有女性的集合的對稱差為所有男性學生和所有女性非學生組成的集合。

基本信息

• 中文名：對稱差
• 英文名：Symmetric difference

• 符號：一般為△或⊕
• 類別：數學函式

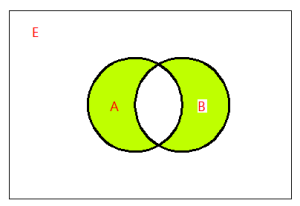
定義

數學上，兩個集合的對稱差是只屬於其中一個集合，而不屬於另一個集合的元素組成的集合。

公式

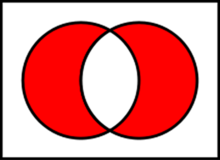對稱差文氏圖表示,紅色區域表示對稱差

對稱差相當於兩個相對補集的並集，即：
AΔB=(A−B)∪(B−A)
也可以表示為兩個集合的並集減去它們的交集：
AΔB=(A∪B)−(A∩B)
或者用XOR運算表示：
AΔB={x:(x∈A)XOR(x∈B)}.
對稱差運算滿足交換律和結合律：
AΔB=BΔA
(AΔB)ΔC=AΔ(BΔC)
在對稱差運算中，空集是單位元，任何元素都是其自身的逆元：
AΔØ=A
AΔA=Ø
綜上可得，採用對稱差運算，任意集合X的冪集是阿貝爾群。由於該群中所有元素都是其自身的負元，這個群實際上是二元域Z2上的向量空間。若X有限，則以其為元素的單元集合構成這個向量空間的基，那么向量空間的維數等於X的元素個數。這種構造方法用於圖論，可定義圖的圈空間。
對稱差相對交集滿足分配律：
A∩(BΔC)=(A∩B)Δ(A∩C)
表明以對稱差作為加法，交集作為乘法，X的冪集是一個環。這是布爾環的一個示例。
對稱差可以在任意布爾代數中定義，寫作
xΔy=(x∨y)∧¬(x∧y)=(x∧¬y)∨(y∧¬x)
這個運算具有用集合中的對稱差相同的性質。